Modèles mathématiques d’épidémies les plus élaborés : pourquoi leurs prévisions initiales sont-elles souvent excessivement pessimistes ?

Les mod­èles math­é­ma­tiques des pandémies, y com­pris ceux con­sid­érés comme les meilleurs, tel celui de l’Imperial Col­lege de Lon­dres, ont sou­vent fourni des prévi­sions ini­tiales exagéré­ment pes­simistes. L’article donne des raisons pos­si­bles de ces erreurs et sug­gère quelques actions qu’il con­viendrait de men­er pour sor­tir de cette situation.

« Up to now, the effects of social dis­tanc­ing have pre­dom­i­nant­ly been stud­ied from a view­point of cen­tral­ly con­trolled action. We argue that it is of equal impor­tance to con­sid­er the self-ini­ti­at­ed reac­tions of indi­vid­u­als in the pres­ence of a con­ta­gious disease. »

Sebas­t­ian Funk, Erez Gilad, Chris Watkins, and Vin­cent A. A. Jansen in Pro­ceed­ings of the Nation­al Acad­e­my of Sci­ences of the USA.

Repères

Le pre­mier essai de mod­éli­sa­tion math­é­ma­tique du développe­ment d’une épidémie date de 1760 (Bernouil­li pour la var­i­ole). Le début du XX^e siè­cle a vu les ten­ta­tives d’Hamer pour la peste (1906) et de Ross pour la malar­ia (1911). Enfin est apparu en 1927 le mod­èle dit com­par­ti­men­tal de Ker­ma­ck (biochimiste) et McK­endrick (médecin mil­i­taire) con­nu par son acronyme SIR. La plu­part des mod­èles actuels en sont issus.

Le modèle SIR : un problème traditionnel de l’antique certificat d’études primaires

Un des prob­lèmes posés tra­di­tion­nelle­ment en fin d’études pri­maires aux élèves qui n’entraient pas en 6^e était celui du cal­cul de niveau d’eau dans un réser­voir ali­men­té par un robi­net et vidé simul­tané­ment à tra­vers une bonde. Dans le cas du mod­èle SIR, on a trois réser­voirs : le pre­mier, con­tenant ini­tiale­ment tout le liq­uide (= la pop­u­la­tion saine) et rem­plis­sant pro­gres­sive­ment les réser­voirs de niveau inférieur (« Infec­tés » et « Rétab­lis et décédés ») à tra­vers un sys­tème de bon­des et de robinets.

Cepen­dant, une dif­férence de taille : dans l’épreuve de feu le CEP, les débits des robi­nets et des bon­des étaient con­stants, alors que dans le mod­èle SIR les débits sont vari­ables et dépen­dent des niveaux dans les réservoirs.

Pour bien saisir les raisons pour lesquelles le SIR et les mod­èles dérivés don­nent des résul­tats sou­vent éloignés de la réal­ité du développe­ment d’épidémies, il con­vient de porter atten­tion à la déf­i­ni­tion pré­cise des paramètres régis­sant leur fonc­tion­nement, tra­di­tion­nelle­ment nom­més β et γ.

On con­sid­ère une pop­u­la­tion N (par exem­ple celle d’un pays ou d’une ville) où les indi­vidus peu­vent être infec­tés par un virus (ou une bac­térie, ou encore un par­a­site). Cette pop­u­la­tion est divisée en 3 « compartiments » :

• S ou Sains Sus­cep­ti­bles d’être infec­tés (nom­bre pra­tique­ment égal à N en début d’épidémie) ;
• I ou Infec­tés (quelques indi­vidus con­t­a­m­inés en début d’épidémie) ;
• R ou Rétab­lis (indi­vidus con­t­a­m­inés puis guéris – et, dans ce dernier cas, con­sid­érés sys­té­ma­tique­ment comme immu­nisés – ou décédés ; réser­voir vide en début d’épidémie).

Chaque indi­vidu infec­té (automa­tique­ment con­sid­éré comme immé­di­ate­ment con­tagieux dans ce mod­èle très sim­ple) a par unité de temps en moyenne κ con­tacts pou­vant théorique­ment trans­met­tre l’infection à d’autres mem­bres de la pop­u­la­tion, donc κ.S/N avec des indi­vidus sus­cep­ti­bles d’être infectés.

Si on appelle τ la trans­mis­si­bil­ité du virus, les I per­son­nes infec­tées con­t­a­mi­nent donc I.κ.τ.S/N indi­vidus par unité de temps, qui de ce fait quit­tent le com­par­ti­ment S. Si on pose β = κ.τ /N on a :

dS/dt = — β S I

S’il y a I infec­tés pour une durée moyenne D, alors par unité de temps I/D indi­vidus migrent du com­par­ti­ment I vers R par guéri­son ou décès. On pose habituelle­ment γ = 1/D

Donc

dR/dt = γ I (Nous revien­drons plus loin sur cette équa­tion « foireuse ».)

Dans ce mod­èle sim­ple, si la durée de l’épidémie n’est pas trop longue, on ne tient pas compte des nou­velles nais­sances. Donc I = N — S – R et par voie de con­séquence dI/dt = — dS/dt – dR/dt.

Ce qui con­duit à :

dI/dt = β S I – γ I

Point impor­tant et qui sera dis­cuté plus loin : on sup­pose dans le mod­èle SIR de base que, entre événe­ments changeant rad­i­cale­ment la prop­a­ga­tion de l’épidémie (con­fine­ment oblig­a­toire, appari­tion d’un vac­cin ou d’un traite­ment effi­caces…) qui oblig­ent à faire de nou­veaux cal­culs, β et γ sont con­stants pen­dant une phase d’épidémie don­née (et dif­férents de ceux d’une épidémie qui serait causée par un autre virus).

Le très médi­atisé taux de repro­duc­tion ini­tial R₀ (nom­bre moyen de cas sec­ondaires pro­duits pen­dant toute la durée de son infec­tion par un infec­tieux placé dans une pop­u­la­tion entière­ment saine) est égal à κτD = βN/ γ. En début d’épidémie S est très voisin de N et la 3^e équa­tion peut alors s’écrire dI/dt = β.N.I – γ.I = γ.(R₀ ‑1).I, équa­tion de forme dI/dt = K.I ayant pour solu­tion I = A.e^Kt.

À con­di­tion que R₀ soit supérieur à 1, l’épidémie se développe ini­tiale­ment à la vitesse d’une expo­nen­tielle d’exposant γ.(R₀-1).t

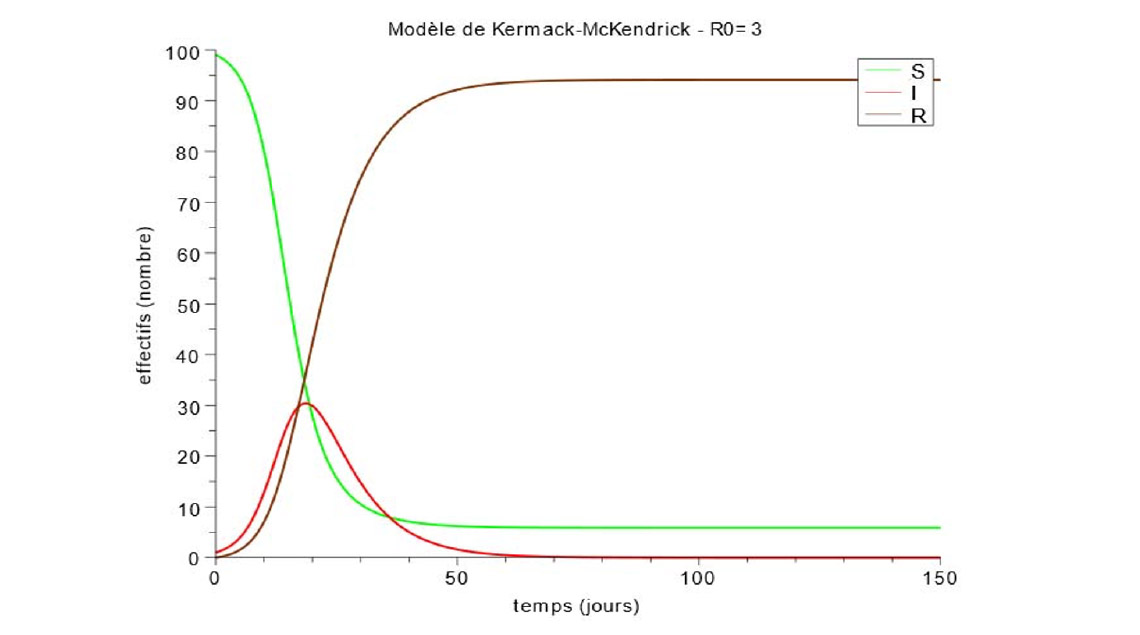
Lorsqu’on sort de cette zone de démar­rage, l’ensemble des équa­tions dif­féren­tielles, même avec β et γ con­stants, n’a pas de solu­tion ana­ly­tique. Il faut avoir recours à un solveur infor­ma­tique pour trac­er les 3 courbes S, I et R en fonc­tion du temps. On obtient pour I une courbe en cloche dis­symétrique, la mon­tée vers I_max étant plus rapi­de que la redes­cente vers 0. Les courbes S et R ont une forme en S dont les asymp­totes don­nent pour S la pop­u­la­tion restée saine en fin d’épidémie et pour R la pop­u­la­tion sor­tie de l’infection (guérie donc immu­nisée, ou décédée).

Les modèles dérivés

Depuis 1927, les chercheurs ont voulu amélior­er ce mod­èle. Les grandes ten­dances sont les suivantes :

• aug­men­ta­tion du nom­bre de com­par­ti­ments (infec­tés récents pas encore con­tagieux, infec­tés con­tagieux avant appari­tion des symp­tômes, sépa­ra­tion des guéris immu­nisés et des décédés, seg­men­ta­tion par tranch­es d’âges, prise en compte des asymp­to­ma­tiques, des nais­sances pen­dant l’épidémie, d’une éventuelle vac­ci­na­tion efficace…) ;
• étab­lisse­ment de « matri­ces de con­tacts » per­me­t­tant d’évaluer les con­séquences de con­tacts spé­ci­fiques à dif­férents con­textes (foy­er, tra­vail, école, prox­im­ité géo­graphique, ren­con­tres de type sportif, cul­turel, confessionnel …) ;
• rem­place­ment de don­nées fix­es par des don­nées prob­a­bilistes afin de met­tre en œuvre des mod­èles stochastiques ;
• util­i­sa­tion de « mod­èles agents » fondés sur l’analyse de la con­duite d’individus.

Les lecteurs qui s’intéressent à cette ques­tion pren­dront con­nais­sance avec intérêt de la syn­thèse con­tenue dans l’article du 2 avril 2020 de Nature : « The sim­u­la­tions dri­ving the world’s response to Covid-19 ».

Les critiques des modèles

Ce qui frappe quand on décou­vre ce domaine est le con­stat d’une prise de con­trôle de fait des amélio­ra­tions pos­si­bles de ces mod­èles par les seuls math­é­mati­ciens, qui alig­nent sou­vent pen­dant des dizaines de pages des suites d’équations pas tou­jours très compréhensibles.

“Les mathématiciens alignent souvent pendant des dizaines de pages des suites d’équations pas toujours très compréhensibles.”

Témoignent de l’incompréhension entre mod­élisa­teurs et médecins réfrac­taires aux équa­tions cer­taines déc­la­ra­tions de l’épidémiologiste français le plus médi­a­tique : « La courbe en cloche (de la Covid-19) est celle typ­ique des épidémies. […] Les épidémies com­men­cent, accélèrent, cul­mi­nent, et elles dimin­u­ent sans qu’on sache pourquoi … C’est un cycle général habituel et on voit que c’est comme ça que se com­porte cette mal­adie. » (Inter­view de fin avril 2020)

« Per­son­nelle­ment, je ne crois pas que la mod­éli­sa­tion math­é­ma­tique pré­dic­tive soit de nature sci­en­tifique, je pense qu’il s’ag­it d’une prophétie mod­erne comme l’a été l’as­trolo­gie à un moment don­né. » (arti­cle sous sa sig­na­ture dans Le Point du 3 mars 2016)

« Tous les gens qui fer­ont des mod­èles pré­dic­tifs sur des mal­adies qu’on ne con­naît pas sont des fous. » (Audi­tion devant la com­mis­sion d’enquête par­lemen­taire, juin 2020)

Le résul­tat est que les mod­élisa­teurs ont générale­ment con­sacré beau­coup plus d’énergie à raf­fin­er la par­tie math­é­ma­tique de leurs travaux qu’à amélior­er la recherche de l’exhaustivité et de la qual­ité des don­nées ali­men­tant leurs mod­èles, atti­tude à la rigueur admis­si­ble si les résul­tats obtenus avaient été bril­lants, mais les récentes et très impor­tantes erreurs des pré­dic­tions des organ­ismes les plus réputés mon­trent que ce n’est pas le cas.

Dans les épidémies réelles, des équations où β est constant ne tiennent pas compte du comportement réel de la population

Égal à κ.τ /N, β peut vari­er au cours du temps :

• κ est le nom­bre moyen de con­tacts de chaque indi­vidu infec­té avec un indi­vidu sain pou­vant théorique­ment débouch­er sur la con­t­a­m­i­na­tion de ce dernier. Il dépend unique­ment de fac­teurs com­porte­men­taux (éventuelle réduc­tion – volon­taire ou con­trainte – du nom­bre de con­tacts, par­tic­i­pa­tion ou non à des réu­nions de groupes d’une cer­taine taille, etc.).
• τ est la trans­mis­si­bil­ité de l’infection. Il dépend à la fois de critères médi­caux (con­ta­giosité du virus) et com­porte­men­taux (ren­con­tre dans un espace con­finé ou en plein air, port ou non de masque, fréquence du lavage des mains, gestes bar­rières, etc.).

La con­ta­giosité du virus peut dépen­dre de fac­teurs externes (humid­ité, tem­péra­ture, éventuelle­ment selon un rythme saison­nier). Elle peut égale­ment évoluer lors d’éventuelles muta­tions de ce virus lors de sa réplication.

Il sem­ble toute­fois que ces muta­tions spon­tanées du virus ne peu­vent avoir un effet glob­al aus­si rapi­de que des change­ments com­porte­men­taux qui inter­vi­en­nent en quelques jours, à mesure que la con­nais­sance de l’épidémie se répand et que les autorités san­i­taires imposent des mesures de pro­tec­tion de la population.

La plu­part des mod­élisa­teurs effectuent des cal­culs avec des β dif­férents avant et après adop­tion d’une déci­sion de type admin­is­tratif, telle que la fer­me­ture des écoles, des salles de spec­ta­cle, le con­fine­ment général­isé, etc. Mais ils ne pren­nent pas en compte la réal­ité du com­porte­ment de la pop­u­la­tion qui prend peur à mesure que les infor­ma­tions alar­mantes sur l’épidémie se répan­dent et qui change pro­gres­sive­ment ses habi­tudes, puis inverse­ment baisse la garde quand le nom­bre d’infectés com­mence à dimin­uer. De façon sur­prenante, il ne sem­ble pas y avoir eu étude d’un mod­èle rel­a­tive­ment sim­ple où β vari­erait de façon con­tin­ue pour tenir compte de ces com­porte­ments à mesure que le temps passe.

“La plupart des modélisateurs ne prennent pas en compte la réalité du comportement de la population.”

Notons que γ peut lui aus­si vari­er au cours du temps, mais unique­ment pour des raisons médi­cales : nou­veaux traite­ments réduisant la durée moyenne d’infection, éventuelles muta­tions du virus.

Prise en compte de β (donc également R₀) variables grâce à l’utilisation d’Excel pour la modélisation

L’utilisation d’Excel pour obtenir les résul­tats d’une mod­éli­sa­tion de type SIR per­met d’introduire très facile­ment des paramètres β (donc aus­si R₀) vari­ant de façon con­tin­ue avec le temps. Cette pos­si­bil­ité, apparem­ment ignorée des spé­cial­istes, est détail­lé dans un autre arti­cle de ce même numéro.

L’hypothèse de β variant pour des raisons comportementales peut expliquer des différences surprenantes entre pays

Lorsque l’épidémie de la Covid-19 est sor­tie de Chine, on en craig­nait un développe­ment par­ti­c­ulière­ment rapi­de dans les pays peu dévelop­pés aux struc­tures médi­cales, en par­ti­c­uli­er hos­pi­tal­ières, très insuff­isantes. Or ce sont les pays occi­den­taux qui ont été ini­tiale­ment les plus touchés.

Bien enten­du les pays peu dévelop­pés présen­tent quelques avan­tages face à cette pandémie, car leur pop­u­la­tion est plus jeune et encore très rurale. On peut y ajouter qu’en rai­son de mul­ti­ples infec­tions antérieures exis­tent peut-être vis-à-vis d’un nou­veau virus des immu­ni­sa­tions croisées de la pop­u­la­tion (rap­pelons qu’il ne s’agit pas d’une notion chimérique : la pre­mière « vac­ci­na­tion » de l’histoire a été l’inoculation du virus de la vac­cine de la vache pour pré­mu­nir de la var­i­ole humaine).

Mais les avan­tages de la jeunesse et de la rural­ité s’estompent peu à peu : dans les dernières décen­nies, la longévité des indi­vidus y a aug­men­té de façon sig­ni­fica­tive et une pro­por­tion de plus en plus impor­tante de la pop­u­la­tion vit en ville, en par­ti­c­uli­er dans des mégapoles aux infra­struc­tures très insuffisantes.

Les mem­bres des sociétés avancées, quant à eux, ont une cul­ture de con­fi­ance exces­sive envers la médecine depuis l’arrivée des antibi­o­tiques et la général­i­sa­tion de nom­breux vac­cins. Ils vivent avec le sen­ti­ment qu’ils pour­ront presque tou­jours béné­fici­er, s’ils con­tractent une mal­adie infec­tieuse, d’un traite­ment effi­cace, d’un coût pour eux réduit ou même nul dans les pays où existe un bon sys­tème d’assurances sociales. Cela peut con­duire à des régres­sions dans cer­taines pré­cau­tions : de nos jours, en France, avant de le rem­plir de lait, on rince sim­ple­ment à l’eau du robi­net un biberon des­tiné à un nour­ris­son, alors qu’il y quelques décen­nies on le lais­sait plusieurs min­utes dans de l’eau en ébul­li­tion, réflexe de par­ents nés avant l’arrivée des antibiotiques.

Dans les pays peu dévelop­pés, en cas d’épidémie pou­vant entraîn­er la mort ou laiss­er de graves séquelles, la peur des habi­tants est vraisem­blable­ment décu­plée par rap­port à celle de pays dévelop­pés : le risque de sat­u­ra­tion du sys­tème de san­té est grand, et y accéder peut avoir un coût exor­bi­tant pour la grande majorité de la pop­u­la­tion. Il est donc pos­si­ble (mais à véri­fi­er …) que cette peur déclenche de très bru­taux réflex­es de prise de dis­tance avec les malades, ce qui pour­rait plus que com­penser l’hygiène médiocre accom­pa­g­nant la vie courante.  

Les carences dans la détermination précoce de β face à un nouveau virus

Pour être en mesure de faire des prévi­sions fiables, il est impor­tant de dis­pos­er dès que pos­si­ble d’une esti­ma­tion fiable de β à par­tir du nom­bre quo­ti­di­en de nou­veaux infec­tés. Or, dans le cas de la Covid‑19 arrivée en Europe fin 2019 ou début 2020, la plu­part des pays ne con­nais­sent tou­jours pas début juil­let 2020 le nom­bre d’individus réelle­ment infec­tés. Il n’est bien sûr pas pos­si­ble de tester régulière­ment l’ensemble de la pop­u­la­tion (à 100 000 tests par jour pour 67 mil­lions de Français, il faudrait presque 2 ans pour un seul test par per­son­ne). Mais, dès la fin de la pénurie de tests qui avait con­traint à en faire béné­fici­er les seules urgences médi­cales, il aurait été judi­cieux d’affecter quo­ti­di­en­nement une petite par­tie des ressources à des tests sur des échan­til­lons médi­cale­ment représen­tat­ifs de la pop­u­la­tion. Les sociétés de sondage utilisent cette méth­ode pour prédire à quelques pour cent près le résul­tat d’élections à venir. À con­di­tion de dis­pos­er de l’aide de spé­cial­istes médi­caux, ces sociétés sont cer­taine­ment capa­bles de définir la com­po­si­tion d’échantillons per­me­t­tant de suiv­re l’évolution de l’infection de l’ensemble de la pop­u­la­tion pen­dant plusieurs semaines.

Actuelle­ment les don­nées les plus fiables sont les nom­bres de décès quo­ti­di­ens dans les hôpi­taux. À par­tir d’évaluations de la majo­ra­tion per­me­t­tant de tenir compte des décès hors hôpi­tal, de la létal­ité de la mal­adie et de la durée moyenne séparant l’infection du décès, il est pos­si­ble d’établir une esti­ma­tion mal­heureuse­ment assez grossière du nom­bre d’infections quo­ti­di­ennes et donc de β.

Le problème posé par l’équation « foireuse » dR/dt = γ I

Cette équa­tion est cen­sée traduire le fait très con­testable que, s’il existe à un cer­tain moment I infec­tés et si la durée de cette infec­tion avant guéri­son ou décès est D, alors par unité de temps I / D indi­vidus (soit γ I) migrent du com­par­ti­ment I vers R.

L’équation est une bonne approx­i­ma­tion en régime qua­si établi, mais cer­taine­ment pas en régime tran­si­toire, en par­ti­c­uli­er lors des pre­miers décès. En effet, si la durée moyenne d’infection est de 20 jours, il suf­fit qu’en début d’épidémie 20 per­son­nes entrent dans I pour qu’en sorte presque immé­di­ate­ment, selon l’équation dR/dt = γ I, une de ces 20 pour aller dans R. Dans la réal­ité, elle ne sera pas encore guérie !

Dans une approche de mod­èle sim­ple beau­coup plus naturelle, il aurait fal­lu con­sid­ér­er que sor­tent à l’instant t de I ceux qui y sont entrés à l’instant (t‑D), ce qui entraîn­erait une équa­tion : dR(t) / dt = — dS(t‑D) / dt. Mais man­i­feste­ment Ker­ma­ck et McK­endrick ont voulu don­ner à leurs équa­tions dif­féren­tielles une allure clas­sique afin d’en déduire des con­séquences par des raison­nements d’analyse math­é­ma­tique pure. Il est amu­sant de not­er que, sans doute un peu gênés d’avoir endossé sans bronch­er une telle équa­tion (qu’à la suite d’un épidémi­ol­o­giste très médi­a­tique nous pour­rions qual­i­fi­er de « foireuse »), les mod­élisa­teurs noient le pois­son pour cam­ou­fler leur long con­formisme en par­lant main­tenant de « dis­cré­tis­er le mod­èle de façon à pou­voir incor­por­er un effet mémoire, car… un indi­vidu qui vient de ren­tr­er dans I a une prob­a­bil­ité faible d’en sor­tir dans l’immédiat », admirable novlangue pour recon­naître que si la durée de l’infection D est fixe, le nom­bre de sor­tants de I à t est le nom­bre de ceux qui sont entrés dans I à (t – D) !

Conclusions

Pour que les mod­èles épidémi­ologiques soient utiles, ils devraient avant tout être, plus qu’une sorte de ter­rain de jeux pour math­é­mati­ciens, le résul­tat d’une véri­ta­ble coopéra­tion mul­ti­dis­ci­plinaire entre médecins, biol­o­gistes, math­é­mati­ciens, psy­cho­logues, physi­ciens ou ingénieurs, insti­tuts de sondage, tout en gar­dant un max­i­mum de sim­plic­ité, et, en cas de mal­adie incon­nue, s’appuyer dès que pos­si­ble sur des éval­u­a­tions quo­ti­di­ennes du nom­bre total de per­son­nes con­t­a­m­inées, guéries et décédées, obtenues par des méth­odes de sondage.

De cette façon pour­raient être évitées des mésaven­tures telles que celle de l’Hôpital Nightin­gale de Lon­dres (500 lits exten­si­ble à 4 000) qui a été instal­lé en cat­a­stro­phe dans un cen­tre de con­grès, à la suite des prévi­sions pes­simistes de l’Imperial Col­lege, et qui n’a pra­tique­ment jamais servi.

---

Articles similaires :

Covid-19 : une mod­éli­sa­tion sim­ple util­isant Excel, acces­si­ble aux non-math­é­mati­ciens et pleine d’enseignements SARS-CoV­‑2 : « Où est caché le loup ? » « Deux­ième vague » Covid-19 : per­spec­tives 2020–2021 Covid-19 : inter­ro­ga­tions sur le mod­èle épidémi­ologique,
Prise en compte de la vac­ci­na­tion et du « vari­ant anglais » Ges­tion de la crise Covid : la manie française de l’uniforme Au cœur de la guerre pour l’importation des masques