Covid-19 : perspectives d’infection par le variant Omicron


L’arrivée du très contagieux variant Omicron remet en cause de façon radicale les projections précédentes, basées sur la vaccination et les caractéristiques d’autres variants. On ne connaît pas exactement le degré de protection contre Omicron apporté par les vaccins actuels ou par l’immunisation résultant d’infections antérieures. De même ne sont pas encore bien connus le degré de dangerosité de ce virus et la proportion d’infectés qui devra être prise en charge par le système hospitalier. La présente note expose une méthode de calcul simple qui permet de balayer une série de scénarios basés sur les hypothèses qui paraissent aujourd’hui les plus probables.
Rappel sur l’historique de la Covid-19
Cette pandémie mondiale a pris en France la forme de 6 vagues successives.
| Date | Vagues | Cause | Cause de la fin |
| Printemps 2020 | 1ère | Virus « 2020 » | 1er confinement |
| Automne 2020 | 2ème | Fin confinement | 2ème confinement |
| Printemps 2021 | 3ème | Variant Alpha (« anglais ») | Début vaccination |
| Eté 2021 | 4ème | Variant Delta (« indien ») | Suite vaccination + passe sanitaire |
| Automne 2021 | 5ème | Fin immunisation premiers vaccinés | 3ème dose |
| Hiver 2021 | 6ème | Variant Omicron (« sud-africain ») | ? |
Le paramètre qui permet de rendre compte du développement d’une épidémie est le coefficient de reproduction de base R0 qui est le nombre de personnes que contamine en moyenne un individu infectieux pendant toute la durée entre son infection et la fin de sa contagiosité, en supposant qu’il est en contact avec une population dont tous les membres sont susceptibles d’être contaminés. L’expérience des confinements, couvre-feux, passes sanitaires, mesures-barrières… a mis en évidence les règles approximatives suivantes dans les pays qui avaient un mode de vie semblable à celui de la France avant mars 2020 :
- un confinement strict de type mars-mai 2020 permet de diviser le coefficient de reproduction de base R0 par 4
- des mesures moins strictes (mesures barrières, couvre-feux, contrôles d’accès à certains lieux…) entraînent une réduction nettement plus faible.
| R0 | ||
| Virus « 2020 » avant mars 2020 | 3 | Valeur observée |
| Variant « 2020 » pendant confinement de type mars-mai 2020 | 0,7 | Valeur observée |
| Variant « 2020 » avec mesures moins strictes | 1 à 1,5 | Valeur observée |
| Variant « Delta » dans les conditions de vie d’avant mars 2020 | 6 | Valeur reconstituée |
| Variant « Omicron » dans les conditions de vie d’avant mars 2020 | 12 | Valeur reconstituée préliminaire |
L’expérience de la vaccination nous a montré que la protection qui en résultait diminuait d’une façon significative après quelques mois. Ceci a entraîné la généralisation de l’injection d’une « 3ème dose ».
L’expérience et le calcul nous ont montré que, dans une population susceptible d’être contaminée simultanément par deux types de virus, il suffisait de quelques semaines pour qu’un nouveau variant de contagiosité deux fois plus forte remplace pratiquement complètement le virus déjà en place.
Covid en 2022 : une épidémie rapidement « 100% Omicron »
Ceci signifie que très rapidement l’épidémie va être « 100% Omicron », ce qui présente pour sa modélisation un avantage et un inconvénient.
L’avantage est la simplification des calculs. En effet (sauf bien sûr si un variant encore plus contagieux qu’Omicron apparaissait) le rôle réel d’une faible proportion subsidiaire de variants autres qu’Omicron sera suffisamment marginal pour que, compte tenu de la valeur incertaine de nombreux autres paramètres, on puisse se contenter début 2022 d’un modèle simulant l’évolution de l’épidémie due au seul Omicron.
L’inconvénient est que, compte tenu du manque de recul, nous ne savons pas s’il y a coïncidence entre la population susceptible d’être infectée par les variants antérieurs (population dont nous avons une idée, même approximative) et celle susceptible de l’être par Omicron. Ceci veut dire que va manquer pendant quelques semaines un paramètre essentiel permettant de rendre compte et si possible d’anticiper l’évolution de l’épidémie « 100% Omicron ».
Modélisation
La définition de R0 permet d’écrire l’égalité très simple qui, indépendamment de toute connaissance mathématique autre que celle des 4 opérations de base, rend compte de l’évolution de l’épidémie au cours du temps :
- Rappel : R0 est le nombre moyen de personnes faisant partie d’une population entièrement contaminable que contamine un individu infectieux pendant toute la durée entre son infection et la fin de sa contagiosité (D jours)
- R0 x I / D est donc est le nombre de personnes faisant partie d’une telle population que contaminent en moyenne I individus infectieux pendant 1 jour
- si en fait parmi une population totale de N personnes seuls S sont contaminables, il faut multiplier la quantité précédente par S/N, probabilité de tomber lors d’une rencontre sur une personne contaminable.
|
Le nombre de nouvelles infections Omicron quotidiennes à l’instant t est donc
Ro(t) x I(t) x S(t) / (D x N) Ro(t) étant le coefficient de base qui peut varier dans le temps en fonction du mode de vie de la population I(t) le nombre de personnes actuellement infectées par Omicron et réputées contagieuses S(t) la population contaminable par Omicron D la durée moyenne en jours (estimée à 10) entre l’infection et la fin de contagiosité d’un malade Omicron N la population totale |
Face à une épidémie Omicron de coefficient de base R0 très élevé il convient d’éviter tout emploi de la traditionnelle notion de « taux de fin d’infection d’une population malade » enseignée dans les cours d’épidémiologie du monde entier et utilisée par un grand nombre de modélisateurs dans des systèmes d’équations différentielles. En effet cette notion appliquée à des populations constituées d’un agrégat d’infectés tombés malades à des dates différentes conduit à des résultats erronés.
C’est pourtant la méthode qu’emploient tous ceux qui partent des équations bien connues de Kermack et McKendrick (1927) censées rendre compte du schéma SIR (division de la population en 3 catégories : – susceptibles d’être infectés, infectés, remis et immunisés (ou décédés) alors que comme l’indique l’annexe de la communication fondatrice de 1927, ces équations sont une simplification qui correspond à ce que les auteurs ont appelé un special case à constant rates de guérison 1. Comme nous l’avons mentionné dans des articles antérieurs, les équations qui représentent de façon correcte l’idée de base du modèle SIR sont celles qui supposent une durée de contagiosité constante entre infection et fin de contagiosité, conduisant à ce que nous avons appelé le modèle SIRtcc (tcc pour temps de contagiosité constant) facile à mettre en œuvre depuis l’arrivée de l’informatique (voir plus loin).
D’autre part l’emploi du calcul infinitésimal n’apporte aucun avantage de précision par rapport à celui d’équations aux différences finies de pas temporel égal à une journée. En effet, aucun intervalle de temps inférieur à la journée n’est pertinent, puisque l’infection correspondante dépend de contacts entre individus, contacts radicalement différents selon l’heure (avec en particulier un fort contraste entre le jour et la nuit).
Enfin, l’emploi de modèles discrets permet d’utiliser des logiciels courants (tableurs) pour modéliser de façon très simple des développements d’épidémies dans des contextes médicaux (début d’épidémie, arrivée de nouveaux variants, vaccinations, perte progressive d’immunité…) et non-médicaux (confinements, couvre-feux, mesures-barrières, restrictions d’accès, quarantaines, modifications spontanées de comportement de la population…) extrêmement fluctuants et ne pouvant être définis facilement par des fonctions mathématiques du temps.
À condition d’avoir des données biologiques fiables (ce qui n’est pas encore le cas aujourd’hui…), cette méthode permet de déterminer facilement dans différentes hypothèses les quantités suivantes, essentielles pour déterminer les politiques sanitaires compatibles avec les ressources hospitalières du pays :
- le nombre maximum quotidien de nouveaux infectés Omicron pendant toute la durée de cette sous‑pandémie
- le nombre maximum d’infectés simultanés Omicron pendant cette même durée
Un premier tableur simple répartit de façon uniforme la contagiosité d’une personne infectée pendant la durée D de son infection.
Un deuxième tableur plus complexe peut tenir compte d’une contagiosité variant de jour en jour pendant la durée D. Cette donnée n’étant pas encore disponible pour Omicron, nous avons utilisé provisoirement une courbe de contagiosité jour par jour entre infection et fin de contagiosité correspondant à un variant antérieur 2.
Données médicales
Les chiffres approximatifs de début décembre, correspondant apparemment à une stabilisation de la sous-épidémie Delta, sont les suivants :
- 1 500 admissions quotidiennes à l’hôpital (d’où 16 000 hospitalisés),
- 300 admissions quotidiennes en réanimation (d’où 3 000 personnes en service de réanimation).
À cette époque, environ 50 000 nouveaux cas étaient détectés chaque jour. Ce chiffre est vraisemblablement très en‑dessous de la réalité. Dans des études antérieures l’Institut Pasteur a estimé qu’il fallait le doubler.
On aurait donc pour la phase de l’épidémie due essentiellement au variant Delta les taux réels suivants :
- entrée à l’hôpital de 1,5 % des nouveaux infectés ; séjour moyen à l’hôpital de 10,7 jours
- entrée en réanimation de 0,3 % des infectés ; séjour moyen en réanimation de 10 jours
Les chiffres correspondants pour le variant Omicron ne sont pas encore connus de façon précise. Les premières évaluations paraissent justifier une division par 2 ou 3 des taux précédents.
Résultats
Nous avons utilisé les 2 tableurs décrits plus haut. Nous avons constaté que le raffinement dans la modélisation du 2ème tableur n’entraînait pas de modification significative des résultats obtenus avec le tableur le plus simple qui est donc celui qui sera utilisé pour générer les courbes qui suivent.
Nous avons simulé une épidémie Omicron :
- de R0 Omicron égal à 6 (compte tenu du mode de vie de la population fin 2021), limite haute des évaluations actuelles que nous avons retenue par précaution (le cas d’un R0 Omicron plus petit est étudié dans la suite de l’article)
- pour plusieurs valeurs supposées de S0 Omicron/N (proportion de la population susceptible d’être infectée par Omicron, c’est-à-dire que ni la vaccination ni une infection-guérison antérieure n’ont immunisé contre ce variant), cette valeur actuellement inconnue de façon précise étant vraisemblablement nettement plus importante que S0 Delta/N (proportion susceptible d’être infectée par Delta).
Actuellement, nous n’avons pas de données quantitatives fiables sur
- la perte progressive avec le temps de l’immunisation contre Omicron dont bénéficient les vaccinés et les infectés par les variants antérieurs (« 2020 », Alpha, Delta),
- le taux d’immunisation réel contre Omicron des 3èmes doses.
Ces 3èmes doses étant actuellement dispensées à un rythme voisin de celui des vaccinations d’il y a 6 mois dont l’immunisation est en train de disparaître, nous supposerons en première approximation que pendant les premières semaines de 2022 l’effet résultant de ces deux facteurs antagonistes sera faible par rapport à celui des immunisations résultant d’une infection par Omicron suivie de guérison et nous n’en tiendrons pas compte dans les calculs.
La courbe qui suit représente le nombre maximal quotidien d’infections calculé à partir de la proportion de la population supposée susceptible d’être infectée par Omicron à l’arrivée de ce virus.
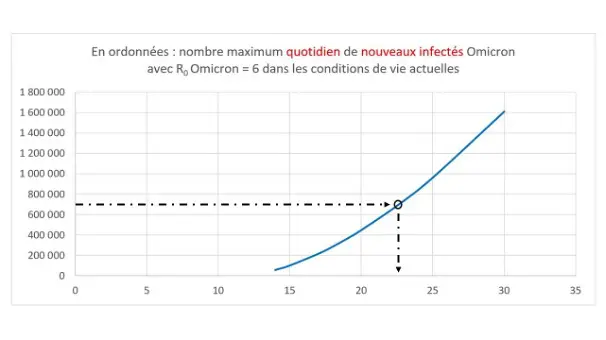
Le nombre quotidien de nouvelles infections constatées par des tests (360 000 le 12 janvier 2022) semble avoir amorcé un plateau. Si nous reconduisons l’estimation antérieure de l’Institut Pasteur (un nombre équivalent d’infections – en particulier asymptomatiques – n’aurait pas été constaté) ceci revient à estimer que le nombre maximum quotidien d’infectés Omicron est environ 700 000.
D’après cette courbe, ceci signifierait qu’au moment de l’apparition d’Omicron environ 22,6 millions 3 de personnes (y compris les enfants) vivant en France n’étaient pas ou plus immunisées vis-à-vis de ce variant (que ce soit par vaccination, infection Covid-19 suivi de guérison ou éventuelle immunité naturelle).
La courbe qui suit représente les conséquences de ce qui précède sur le système hospitalier.
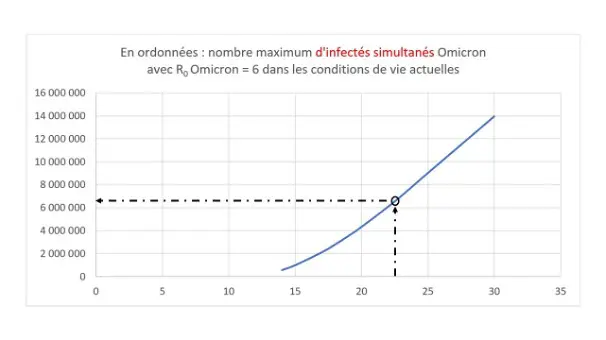
Lecture : Si 22,6 millions de personnes vivant en France n’étaient pas ou plus immunisées vis-à-vis d’Omicron à son arrivée, et si les conditions de vie maintiennent R0 Omicron aux alentours de 6, le nombre maximum d’infectés simultanés sera d’environ 6,7 millions.
Ceci a les conséquences suivantes sur les besoins de capacité hospitalière :
|
R0 = 6 |
Si un infecté Omicron demande 2 fois moins de ressources hospitalières qu’un infecté Delta | Si un infecté Omicron demande 3 fois moins de ressources hospitalières qu’un infecté Delta |
|
Pic des hospitalisations simultanées |
54 000 |
36 000 |
|
Pic des réanimations simultanées |
10 000 |
6 700 |
Note importante : ces nombres n’incluent pas les infectés Delta, qui devraient avoir pratiquement disparu au moment du pic des infections Omicron.
Influence de nouvelles mesures « non-pharmaceutiques »
Nous avons établi les mêmes courbes dans le cas d’une réduction de 20 % de R0 Omicron par de nouvelles mesures dites « non‑pharmaceutiques » : réduction du nombre de contacts et de la probabilité d’infection lors de chacun de ces contacts.
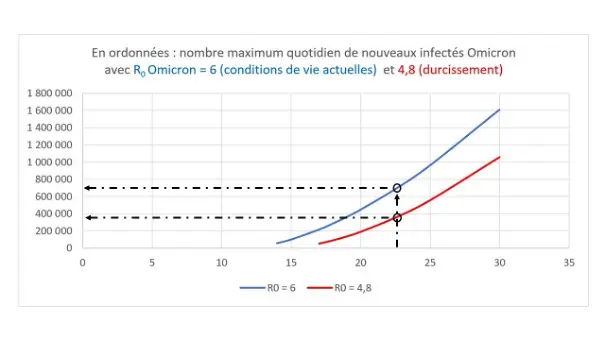
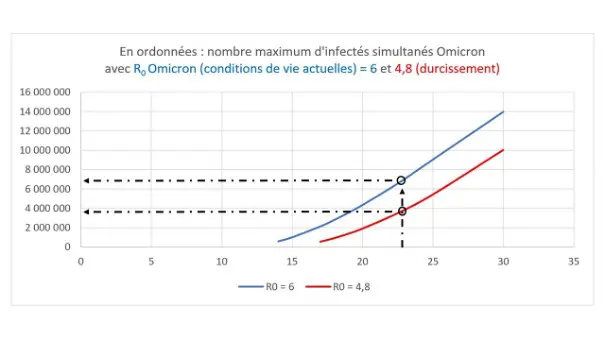
Pour une même population de 22,6 millions de personnes susceptibles d’être contaminées par Omicron, la réduction de 20% de R0 Omicron réduirait de 700 000 à 370 000 le nombre maximal quotidien de nouveaux infectés et de 6,7 à environ 3,6 millions le nombre maximum d’infectés simultanés.
Ceci a les conséquences suivantes sur les besoins de capacité hospitalière :
|
R0 = 4,8 (réduction de 20 %) |
Si un infecté Omicron demande 2 fois moins de ressources hospitalières qu’un infecté Delta | Si un infecté Omicron demande 3 fois moins de ressources hospitalières qu’un infecté Delta |
|
Pic des hospitalisations simultanées |
29 000 |
19 000 |
|
Pic des réanimations simultanées |
5 400 |
3 600 |
Note importante : ces nombres n’incluent pas les infectés Delta, qui devraient avoir pratiquement disparu au moment du pic des infections Omicron.
Influence de la vaccination
Les projections qui précèdent montrent qu’une conjonction des hypothèses les plus défavorables sur l’immunisation réelle de la population contre le variant Omega risque d’amener à une situation critique. Par précaution la politique vaccinale actuelle, dont nous ne pouvons pas encore mesurer l’efficacité réelle contre ce variant, doit donc être complétée dès maintenant par des mesures dites « non‑pharmaceutiques » à ajuster en permanence à l’évolution de l’épidémie Omicron. Par chance l’expérience et les calculs très simples que nous avons présentés montrent que l’effet de ces mesures, à défaut d’être pérenne, est extrêmement rapide et puissant.
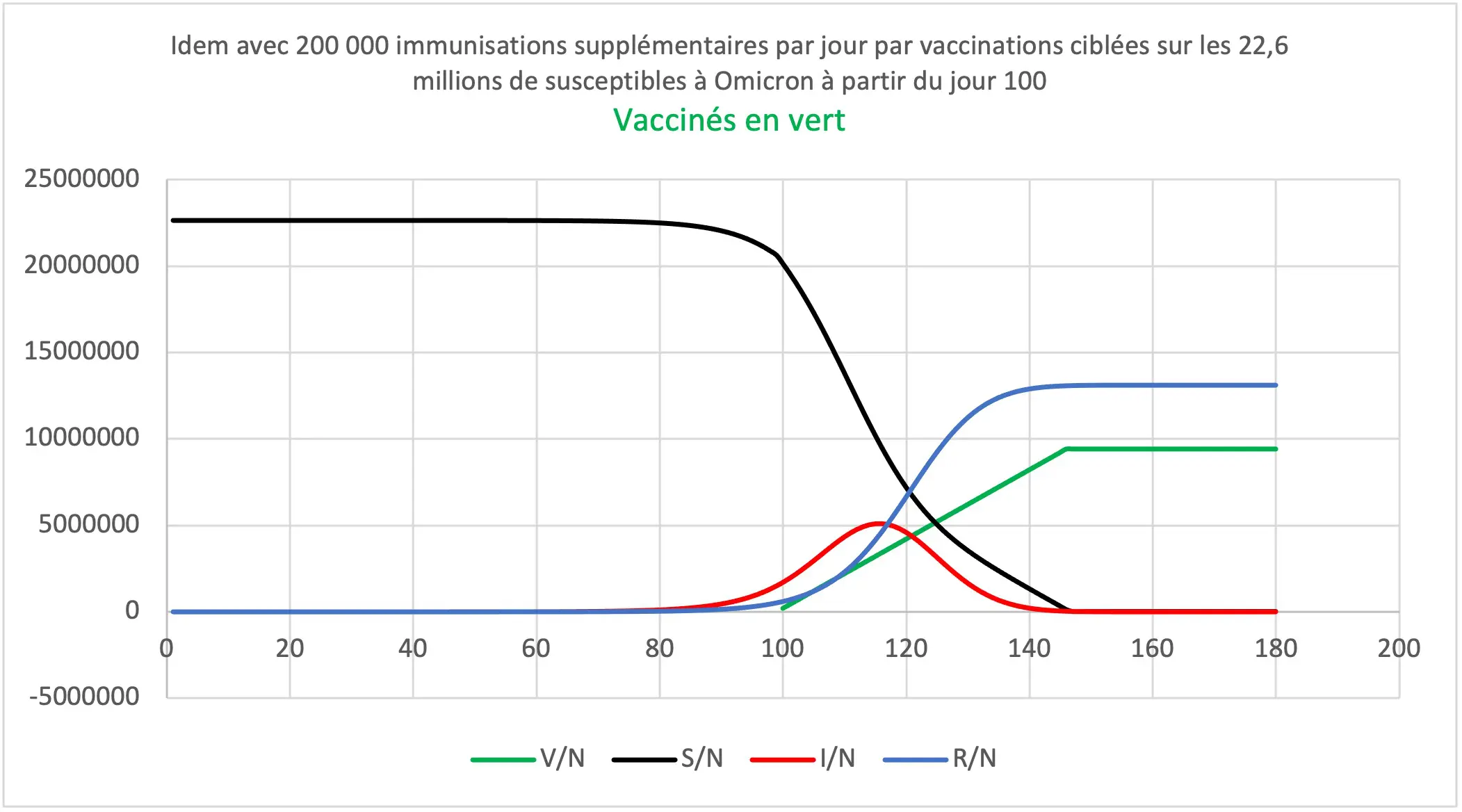
L’annexe jointe montre qu’une hypothétique vaccination ciblée immunisant 200 000 personnes supplémentaires par jour serait trop tardive pour provoquer une baisse radicale des séjours à l’hôpital pendant les prochaines semaines. En revanche elle préparerait à une remontée de R0 par retour progressif à une vie normale.
ANNEXE
Influence d’une intensification de la vaccination
Hypothèse de 200 000 immunisations quotidiennes supplémentaires par vaccinations ciblées sur les 22,6 millions de susceptibles à Omicron
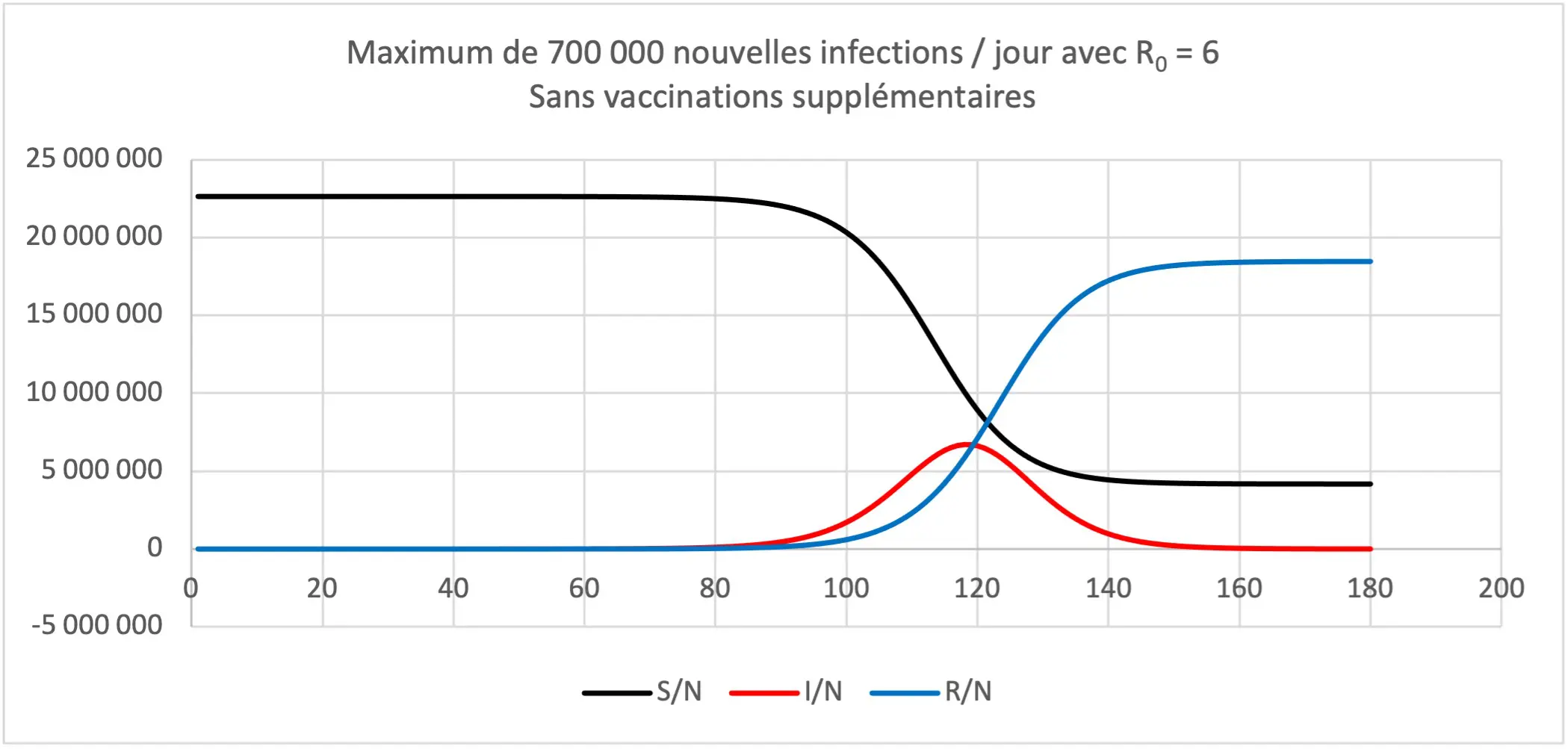
Ordonnées : nombre d’individus « susceptibles d’être infectés », « infectés », « rétablis ou décédés »
1. Kermack, W. O., McKendrick, A. & Walker, G. T. A contribution to the mathematical theory of epidemics. Proc. R. Soc. A 115, 700–721. https://doi.org/10.1098/rspa.1927.0118 (1927) Pages 712–713
2. « Back to the roots : a discrete Kermack-McKendrick model adapted to Covid-19 » Matthias Kreck (Université de Bonn) et Ehrard Scholz (Université de Wuppertal) Pages 9–11
3. On consultera avec intérêt le site https://corona-circule.github.io/lettres/ qui a décidé d’adopter le SIRtcc et qui arrive, après intégration des effets de la vaccination, à un résultat très voisin (24 millions) du nombre de personnes vivant en France susceptibles d’être infectées par Omicron.




2 Commentaires
Ajouter un commentaire
Bonsoir, que se passe-t-il si D est égal à 5, valeur beaucoup plus probable que 10 ?
En utilisant le tableur à contagiosité constante pendant une durée d’infection/contagiosité de 5 jours, on trouve que correspondent à un pic de 700 000 nouvelles infections par jour un maximum de 3,4 millions d’infectés simultanés pour une population non immunisée contre Omicron de 19,1 millions (au lieu de 6,7 millions d’infectés simultanés pour une population non immunisée de 22,6 millions si on part d’une infection/contagiosité de 10 jours). L’intérêt n’est pas dans les chiffres après la virgule, mais de montrer qu’avec les incertitudes actuelles sur la hauteur du pic de nouvelles infections par jour, la durée D, les pourcentages d’infectés qui auront besoin de soins à l’hôpital (éventuellement en réanimation) il y a un risque de se trouver en limite de capacité du système hospitalier dont la vaccination ne permet pas de s’affranchir à court terme.
Ce qui serait intéressant est d’avoir la courbe de contagiosité entre le jour d’infection et la fin de la contagiosité pour Omicron, ce qui permettrait un calcul plus précis avec ce que j’ai appelé le 2ème tableur (1 colonne par jour après l’infection).