L’universalité des formes fractales dans la nature

La mise en évi­dence par Man­del­brot, dans les années soix­ante-dix, de l’existence fréquente de géométries frac­tales dans la nature, est un des développe­ments sci­en­tifiques les plus remar­quables de la sec­onde moitié du XXe siè­cle. On retrou­ve les mêmes formes dans des sit­u­a­tions physiques, chim­iques ou biologiques très différentes.

Une nouvelle géométrie fractale

C’est à Benoît Man­del­brot (44), dis­paru en octo­bre 2010, que l’on doit un nou­v­el intérêt pour la géométrie dont on avait pen­sé, un peu vite, qu’elle avait dit son dernier mot. C’est en effet Man­del­brot qui a dégagé les con­cepts de la géométrie frac­tale, con­cepts per­me­t­tant de décrire des objets hiérar­chiques de forme très irrégulière. C’est lui, qui, pressen­tant l’im­por­tance de cette syn­thèse, a créé le mot même de fractale.

Dans la géométrie clas­sique, une ligne est un objet à une dimen­sion, une sur­face un objet à deux dimen­sions, un vol­ume un objet à trois dimen­sions. Nous sommes donc habitués à des objets dont la dimen­sion est un nom­bre entier 1, 2, ou 3. S’il se trou­ve dans la nature des objets qui puis­sent être décrits par une dimen­sion qui ne soit pas un nom­bre entier, on s’at­tend à ce que leurs pro­priétés dépen­dent de cette même dimen­sion. Ces objets exis­tent, ce sont les objets ” frac­tals “, et dis­ons pour sim­pli­fi­er que l’on appelle une “frac­tale” un objet dont la géométrie peut être décrite par une dimen­sion non entière.

Une ” frac­tale ” est un objet dont la géométrie peut être décrite par une dimen­sion non entière

La mise en évi­dence par Man­del­brot dans les années soix­ante-dix, de l’ex­is­tence fréquente de géométries frac­tales dans la nature, est un des développe­ments sci­en­tifiques les plus remar­quables de la sec­onde moitié du XXe siè­cle. Jusqu’i­ci les formes géométriques trop com­plex­es ne pou­vaient être décrites autrement que par leurs images ou par leur car­togra­phie. Pen­sons aux nuages, aux côtes rocheuses, aux mon­tagnes, aux poumons, aux vais­seaux san­guins, aux racines d’une plante.

Une dimension fractionnaire

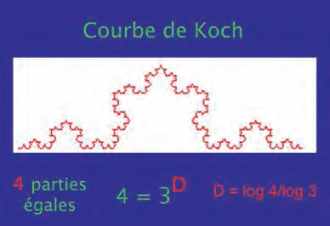
Pour car­ac­téris­er sim­ple­ment une géométrie décrite par une dimen­sion non entière, repor­tons-nous à la fig­ure ci-après. On y voit un cube de côté a. Ce cube peut être divisé en 8 petits cubes de côté a/2. Or un cube est un vol­ume donc un objet à 3 dimen­sions et l’on remar­que que 8 est égal à 23. Ce 3, qui est ici un exposant, est bien la dimen­sion d’un vol­ume que l’on mesure en mètres cubes.

Plus bas, on voit une ” courbe de Koch”. C’est un objet de forme com­pliquée qui est con­stru­it comme indiqué. Mais pour com­pliqué qu’il soit, on peut le divis­er en 4 frag­ments iden­tiques dont la taille est 1/3 de la taille ini­tiale. De la même façon que pour le cube, on peut remar­quer que 4 est égal à 3 (log4/log3). Ce nom­bre log4/log3 (env­i­ron 1,26) joue le rôle d’une dimen­sion comme le nom­bre 3 est la dimen­sion d’un volume.

Autre remar­que, chaque petit cube est sem­blable au cube entier s’il est dilaté (agran­di) d’un fac­teur 2. De même chaque 1/4 de la courbe de Koch est iden­tique à la courbe entière s’il est agran­di d’un fac­teur 3. C’est ain­si que l’on peut intro­duire sim­ple­ment le con­cept de dimen­sion non entière ou de dimen­sion frac­tion­naire ou fractale.

Con­serv­er les formes La notion de dimen­sion frac­tion­naire s’ap­plique aux objets qui pos­sè­dent une simil­i­tude interne : c’est la pro­priété d’une par­tie d’un objet d’être sem­blable à l’ob­jet lui-même à une dilata­tion près. C’est vrai du cube et de la courbe de Koch, mais c’est aus­si vrai des branch­es d’un chou-fleur qui ressem­blent à un chou-fleur entier à une dilata­tion près. Une géométrie qui présente cette pro­priété de simil­i­tude interne est qual­i­fiée d’au­to ou de self-sim­i­laire. On par­le dans tous ces cas de dimen­sions frac­tales. Une telle géométrie est ” invari­ante d’échelle”, ce qui veut dire que quand on change d’échelle d’ob­ser­va­tion, on con­serve les formes.

Déterministe ou aléatoire

À l’o­rig­ine, ce sont des expéri­ences de physique sur les tran­si­tions de phase du sec­ond ordre qui ont induit l’idée d’in­vari­ance d’échelle chez Fis­ch­er, Kadanoff et Wil­son dans les années 60–70 (Ken Wil­son a util­isé cette notion dans sa théorie des tran­si­tions de phase du sec­ond ordre et a reçu le prix Nobel 1982 pour ces travaux). Cette invari­ance d’échelle existe aus­si dans les polymères (travaux de P.-G. de Gennes dans les années 70–80, autre prix Nobel).

Notons que la simil­i­tude interne peut être exacte, comme dans les deux cas de la fig­ure, ou approx­i­ma­tive pour les branch­es d’un chou-fleur qui ne sont pas exacte­ment iden­tiques. Par agran­disse­ment, chaque branche ressem­ble au chou-fleur entier sans le repro­duire exacte­ment. Suiv­ant les cas, on par­lera de frac­tales déter­min­istes ou aléatoires.

L’ubiquité des fractales

En 1988 parais­sait un livre d’un math­é­mati­cien anglais tra­vail­lant aux États-Unis, Michael Barns­ley, dont le titre était Frac­tals Every­where. La géométrie frac­tale a été observée dans un grand nom­bre de sys­tèmes. Cela va d’ob­jets de la physique “sub­mi­cromique” comme des agré­gats atom­iques, des fronts de dif­fu­sion dans les soudures ou la struc­ture des aéro­gels, jusqu’à la répar­ti­tion des galax­ies dans l’u­nivers en pas­sant par la forme des côtes marines et des montagnes.

La géométrie frac­tale peut s’ob­serv­er dans les galax­ies ou les côtes marines

Y aurait-il donc une sig­ni­fi­ca­tion unique à l’ap­pari­tion de ces géométries dans des con­textes aus­si divers ? Non, mais avant de répon­dre, il con­vient de se deman­der pourquoi nous seri­ons sur­pris de l’ex­is­tence de cette géométrie dans la nature. On sait que la symétrie joue dans les phénomènes physiques un rôle fon­da­men­tal. Les symétries sont cer­taines pro­priétés d’in­vari­ance des lois de la physique qui se véri­fient quand un sys­tème subit une trans­for­ma­tion géométrique donnée.

Quand on recherche la nature la plus fon­da­men­tale des inter­ac­tions physiques, on y retrou­ve tou­jours des pro­priétés de symétrie comme c’est le cas de la cor­re­spon­dance entre la matière et l’an­ti­matière. Dans cette optique, la géométrie frac­tale appa­raît comme la géométrie adap­tée à la symétrie de dilata­tion ou d’in­vari­ance d’échelle. Il n’y a, au fond, pas plus lieu de s’é­ton­ner de l’ap­pari­tion de la géométrie frac­tale qu’il n’y a lieu de s’é­ton­ner de la péri­od­ic­ité du réseau cristallin du chlorure de sodium.

Pour s’y recon­naître un peu mieux dans cette mul­ti­tude de sys­tèmes ou de phénomènes, on peut ranger les frac­tales dans quelques caté­gories essentielles.

La géométrie frac­tale serait la géométrie du cal­cul des probabilités

Les systèmes dynamiques non linéaires

La pre­mière caté­gorie de phénomènes dans lesquels on observe, et quelque­fois démon­tre, l’ex­is­tence de frac­tales est l’é­tude des sys­tèmes dynamiques non linéaires. Dans le chaos déter­min­iste, des sys­tèmes très sim­ples, et dont le fonc­tion­nement est stricte­ment causal, sont sus­cep­ti­bles de pos­séder des états apparem­ment aléa­toires. La géométrie frac­tale des attracteurs étranges appa­raît ici fréquem­ment. La tur­bu­lence entre, elle aus­si, dans cette catégorie.

Les phénomènes d’interfaces naturelles

La sec­onde caté­gorie de phénomènes où inter­vi­en­nent des frac­tales est celle des phénomènes d’in­ter­faces naturelles (alvéoles pul­monaires, racines des plantes, bassins flu­vi­aux, réseau san­guin). Il faut pren­dre ici le mot d’in­ter­face dans un sens très général. Ce peut être l’in­ter­face entre deux milieux, c’est alors une vraie sur­face, par exem­ple la sur­face des alvéoles pul­monaires qui sépare l’air du sang dans les poumons des mam­mifères, 140 m² chez l’homme. Dans ce cas, la dimen­sion frac­tale de la sur­face d’échange entre air et sang est proche de 3, celle d’un vol­ume.

Les phénomènes aléatoires

Opti­miser dans un vol­ume donné
L’in­ter­face peut aus­si être l’in­ter­face entre une sur­face, comme l’en­trée de la tra­chée, et un vol­ume, celui des poumons. Com­ment con­stru­ire donc une inter­face entre une sur­face et un vol­ume ? La nature a résolu ce prob­lème par l’in­ter­mé­di­aire d’un arbre, ici l’ar­bre bronchique qui irrigue le vol­ume à par­tir d’une sur­face. Lui aus­si est de dimen­sion 3. Tout cela con­cerne les sys­tèmes dans lesquels un proces­sus d’échange ou de dis­tri­b­u­tion doit être opti­misé dans un vol­ume donné.

La troisième caté­gorie de frac­tales appa­raît dans l’é­tude des phénomènes aléa­toires. Dans ce sens, on peut dire que la géométrie frac­tale serait la géométrie du cal­cul des prob­a­bil­ités, un peu au même titre que la géométrie des courbes dans le plan cor­re­spond à l’é­tude des équa­tions algébriques F (x, y) = 0.

Les exem­ples sont nom­breux. Citons la tra­jec­toire du mou­ve­ment brown­ien, l’a­gré­ga­tion lim­itée par la dif­fu­sion mon­trée sur la fig­ure ci-dessus, les fronts de dif­fu­sion dans les soudures, les vols de Lévy, la per­co­la­tion, les frac­tures, beau­coup de sur­faces rugueuses, la ” crit­i­cal­ité” auto-organ­isée, cer­tains fronts de cor­ro­sion, le tracé des fluc­tu­a­tions bour­sières, etc., sont des exem­ples de cette géométrie née du hasard. Je pense que ce qui est tout à fait fécond et nou­veau, c’est l’idée même qu’à la théorie des prob­a­bil­ités puisse cor­re­spon­dre une géométrie que l’on puisse décrire quantitativement.

Il est clair d’après ces nom­breux exem­ples, cer­tains exacts et d’autres seule­ment con­jec­turés, que la notion de ” géométrie des prob­a­bil­ités ” s’ap­plique bien aux géométries frac­tales. Il sem­ble donc bien aujour­d’hui que la symétrie de dilata­tion, représen­tée par la géométrie frac­tale, soit sou­vent liée au hasard, en fait plus par­ti­c­ulière­ment à ses réal­i­sa­tions et non à ses moyennes.

Le hasard maîtrisé

Jusqu’i­ci le cal­cul des prob­a­bil­ités ne s’in­téres­sait qu’à déter­min­er la quan­tité de prévis­i­ble dans l’im­prévis­i­ble. L’élar­gisse­ment de son champ à la géométrie d’une réal­i­sa­tion d’une suite d’événe­ments aléa­toires con­stitue, à mon sens, une ouver­ture immense et un des grands suc­cès des fractales.

À cela s’a­joute le par­a­digme suiv­ant : si ces sys­tèmes aléa­toires sont frac­tals et donc hiérar­chiques, on peut penser que leurs pro­priétés sont essen­tielle­ment dom­inées par le car­ac­tère frac­tal de cette hiérar­chie (la dimen­sion frac­tale) et que des frac­tales déter­min­istes de même dimen­sion auraient les mêmes pro­priétés. Si cela est vrai, ceci veut dire que, dans ce sens, le hasard est maîtrisé, il a fourni l’essen­tiel de sa com­plex­ité en con­stru­isant des frac­tales. Ce par­a­digme, qui a dom­iné mon intérêt per­son­nel pour ces géométries, est véri­fié pour les élec­trodes (travaux avec Mar­cel Filoche), les catal­y­seurs et les mem­branes fractales.

Quelques jalons
Il existe main­tenant quelques jalons fer­mes à cette idée de frac­tale en tant que ” géométrie du cal­cul des probabilités “.
Citons, par exem­ple, des démon­stra­tions où la tra­jec­toire du mou­ve­ment brown­ien pos­sède une dimen­sion égale à 2 et où les ” vols de Lévy ” d’ex­posants D for­ment des tra­jec­toires de dimen­sion D.
Dans les années 1980, Benoît Man­del­brot a con­jec­turé que la dimen­sion frac­tale du bord extérieur du mou­ve­ment brown­ien plan était égale à 4/3. Cela a été démon­tré par Lawler, Schramm et Wern­er, et a valu à Wen­delin Wern­er sa médaille Fields en 2006.
Nous avions, quant à nous (avec Jean-François Gouyet et Michel Rosso), con­jec­turé en 1985 que la fron­tière extérieure de l’a­mas de per­co­la­tion pos­sé­dait une dimen­sion égale à 7/4. Cela a été démon­tré au début des années 2000 par Stanislav Smirnov qui a reçu la médaille Fields en 2010.

Un pouvoir d’amortissement

Une autre caté­gorie de phénomènes est liée au pou­voir d’amor­tisse­ment des struc­tures frac­tales. Ain­si, les études menées à l’É­cole poly­tech­nique ont démon­tré qu’une cav­ité acous­tique dont la sur­face serait une frac­tale math­é­ma­tique serait infin­i­ment amor­tie. De cela on peut déduire que la frac­tal­ité de cer­taines côtes marines serait auto-amortie.

La puis­sance disponible de la mer con­duirait à une autolim­i­ta­tion de l’ef­fi­cac­ité de l’érosion

Cette frac­tal­ité serait due au fait que la mer, attaquant les points les plus faibles d’une terre aléa­toire, pro­duirait par éro­sion une côte irrégulière qui l’amor­ti­rait davan­tage. Bien enten­du, le hasard con­tin­ue à jouer un rôle par le fait que le rivage érodé est con­sti­tué d’élé­ments de résis­tances aléa­toires. Mais ce sont les con­di­tions physiques, ici la puis­sance disponible de la mer, qui con­duirait à une autolim­i­ta­tion de l’ef­fi­cac­ité de l’éro­sion. Ici, il s’ag­it d’un amor­tisse­ment mécanique.

Un autre cas est le cas de l’at­taque chim­ique d’un solide désor­don­né par un agent cor­rosif dont le poten­tiel chim­ique s’épuise au fur et à mesure que l’at­taque se pro­duit. Ici aus­si le hasard con­tin­ue à jouer un rôle, mais le proces­sus de cor­ro­sion est autolim­ité. C’est une frac­tal­ité auto-organ­isée car c’est l’évo­lu­tion spon­tanée de ces sys­tèmes qui les con­duit vers une struc­ture fractale.

L’universalité des fractales aléatoires

Le sens du mot “uni­ver­sal­ité” varie suiv­ant le con­texte. Le sens qui nous con­cerne est celui de la physique sta­tis­tique pro­posé par Fis­ch­er, Kadanoff et Wil­son. Il dit que cer­tains sys­tèmes pos­sè­dent des pro­priétés indépen­dantes de leur nature microscopique.

Une autre classe d’u­ni­ver­sal­ité est celle de la per­co­la­tion en gra­di­ent. C’est la géométrie d’une soudure à 2 dimen­sions avec une dimen­sion frac­tale de 7/4 (démon­trée récem­ment par Pierre Nolin et Wen­delin Wern­er). Dans une modal­ité un peu dif­férente, ce peut être aus­si la géométrie d’une fig­ure de cor­ro­sion ou la géométrie (cal­culée) d’un rivage soumis à l’éro­sion marine. Ici la dimen­sion frac­tale vaut exacte­ment 4/3.

Il s’ag­it de géométrie. De même que la terre est ronde, un peu comme une orange, ou comme une boule de pétanque, ces objets, tous dif­férents, ont une même géométrie, la sphère, forme uni­verselle. Ici “même géométrie” se traduira par “même dimen­sion frac­tale”. Cette notion d’u­ni­ver­sal­ité sur­git de l’ex­a­m­en de sit­u­a­tions expéri­men­tales très dif­férentes qui présen­tent des géométries irrégulières à toute échelle (frac­tales) mais dont les analo­gies de forme sont évidentes.

Ain­si des dépôts élec­troly­tiques, des formes d’in­jec­tion d’eau dans du plâtre, la forme d’une pré­cip­i­ta­tion spon­tanée, la crois­sance d’une colonie bac­téri­enne présen­tent des géométries très proches, la forme d’une pré­cip­i­ta­tion spontanée.

Ce qui est com­mun entre ces expéri­ences, c’est leur géométrie qui pos­sède donc un car­ac­tère uni­versel. On retrou­ve les mêmes formes dans des sit­u­a­tions physiques (ou chim­iques ou biologiques) très dif­férentes. On définit ain­si une classe d’u­ni­ver­sal­ité qui regroupe des phénomènes dif­férents décrits par le même type de géométrie. Dans ce cas, il s’ag­it de la géométrie de l’a­gré­ga­tion lim­itée par la dif­fu­sion dont le nom provient du mécan­isme de crois­sance à tra­vers lequel il a été intro­duit par Tom Wit­ten et Leonard Sander en 1981. La dimen­sion frac­tale est proche de 1,7.

Une cristallographie du hasard

Regrouper toutes ces géométries aléa­toires dans dif­férentes class­es d’u­ni­ver­sal­ité, c’est un peu créer ce qui pour­rait s’ap­pel­er une cristal­lo­gra­phie du hasard. Ain­si, ces con­cepts ont mod­i­fié la vue et les per­spec­tives que l’on avait sur de nom­breux phénomènes naturels. Est-il meilleur exem­ple de la force de l’idée d’u­ni­ver­sal­ité de cer­taines géométries frac­tales que la cara­pace du coquil­lage Cym­bi­o­la innexa (Reeve) où l’on voit aus­si le tri­an­gle de Sier­pin­s­ki, fig­ure math­é­ma­tique qui date du début du siè­cle dernier ?

Mais ce tri­an­gle de Sier­pin­s­ki on le retrou­ve (caché) dans le tri­an­gle de Pas­cal en rem­plaçant tous les nom­bres impairs par des points et en sup­p­ri­mant tous les nom­bres impairs. C’est Hans Mein­hardt qui a mon­tré que cer­tains types de réac­tions chim­iques en présence de dif­fu­sion fab­ri­quaient spon­tané­ment des géométries de ce type. Qui aurait cru qu’en­tre cer­taines des pro­priétés du tri­an­gle de Pas­cal et la déco­ra­tion de cer­tains coquil­lages il y ait quelque chose de com­mun et que ce com­mun soit frac­tal ? C’est bien cela, l’u­ni­ver­sal­ité des frac­tales. Un grand mer­ci à Benoît Man­del­brot de nous avoir mis sur des chemins si riches.

Quelques excès
L’u­biq­ui­té des frac­tales a don­né lieu à quelques excès et l’on a vu paraître vers la fin des années qua­tre-vingt des arti­cles se bas­ant sur des car­ac­téri­sa­tions frac­tales peu fiables. À cela s’a­joute que, dans cer­tains cas, les car­ac­téri­sa­tions frac­tales sont directe­ment con­di­tion­nées par la qual­ité des don­nées, don­nées qui elles-mêmes évolu­ent dans le temps avec les tech­niques instru­men­tales. C’est le cas en ce qui con­cerne la très actuelle ques­tion de la dis­tri­b­u­tion frac­tale des galax­ies, sujet pas­sion­nant et en con­stante évolution.

---

Articles similaires :

Pren­dre au sérieux les langues dans l’entreprise Pourquoi pas nous ? Grandes Écoles : Le mod­èle uni­ver­si­taire des sociétés en développement Pour un traité d’interdiction totale des armes nucléaires Chô­mage des jeunes : réal­ités, con­séquences, remèdes Tra­vail et salaire, les poly­tech­ni­ciens sont très satisfaits !