Mathématiques, beauté, dépaysement soudain

Dépaysements
Superbes et pédagogiques, des vidéos vivifiaient le parcours, menant le visiteur vers de soudains dépaysements. Ainsi celle qui montrait le survol d’une forêt par un perroquet corseté par la formule d’aérodynamique de Bernoulli : éphémère chef‑d’œuvre, gestuelle animalière injectée de rationnel.
Pour réussir cette exposition, Hervé Chandès, directeur général de la Fondation Cartier, a fait appel à quelques puissants ingrédients : des mathématiciens de très haut niveau, des artistes de très grand talent, une collaboration étroite mais enjouée entre ceux-ci et ceux-là, une sorte de chorégraphie des esprits.
Quatre mystères
Une cinquantaine de textes très brefs révélait sur vingt-cinq siècles la lente mais inexorable montée de la connaissance de l’univers en Occident. Certains traduisaient la prise de conscience par l’homme de cette nature, d’autres exprimaient les limites de ses propres raisonnements, puis leur caractère peu à peu dépouillé d’anthropocentrisme. Pour Misha Gramov, mathématiques et physique nous mènent vers quatre « mystères ». D’abord celui des lois de la physique : comment la structure isotrope due au choc initial « se dissipe au fur et à mesure que l’univers est déchiffré par l’observation humaine ».
L’harmonie cachée vaut mieux que l’harmonie visible (Héraclite)
Puis il y a le mystère de la vie, irruption d’une structure de complexité « condensée dans des îlots de réel ». Troisième mystère, celui du cerveau, « masse de matière organique et apparemment amorphe, capable, en suivant les lois de la physique, de sélectionner une réponse adéquate dans un ensemble » inouï de possibilités. La modélisation permet d’approcher ces trois énigmes. Enfin, quatrième mystère, celui de la structure mathématique : « Comment le cerveau arrive à l’élaborer, à partir du chaos des inputs externes1. »
Bonheur et émerveillement
Conçue par un artiste japonais, une surface de révolution à courbure négative marquait de sa beauté l’un des espaces. À côté, une vidéo montrait le bonheur professionnel qu’éprouvent des mathématiciens et physiciens de haut vol.
Équipe de pilotage
Animée par Jean-Pierre Bourguignon (66), elle a réuni la probabiliste Nicole El Karoui, les deux « médailles Fields » Alain Connes (l’un des pères de la géométrie non commutative) et Cédric Villani (connu pour son apport à la théorie cinétique des gaz), Misha Gromov, Sir Michaël Atiyah, Don Zagier, Carolina Canales Gonzalez et Giancarlo Lucchini.
Bonheur rayonné par chacun des membres du Comité de pilotage quand il parlait de son métier, des temps de découverte, des temps morts ou de gestation, de la joie constante d’explorer le réel et même son filigrane mathématique.
Émerveillement de Nicole El Karoui quand, terminant son témoignage sur ses recherches en probabilité, elle s’émerveillait des facettes si diverses du hasard qu’elle reliait à la diversité de ses cinq enfants. Quel est le « moteur de recherche » de ces témoins ? Le goût de l’aventure, de la recherche de la vérité et de la beauté, la joie de l’exploration.

Diffusion de la chaleur (équation de Fourier), image du film de Beatriz Milhazes et BUF,
Les Paradis mathématiques, 2011. Création BUF.
Enfin, sur fond de ciel nocturne, les écrits de Poincaré formaient des ensembles ayant chacun son thème et son unité. En somme, des « constellations » dans un ciel mathématique.
Muse des sciences
Quel est donc ce cerveau, qui nous aide ainsi à tant connaître cet univers, à pratiquer pareille introspection intellectuelle, et qui fait parfois du mathématicien moderne un collègue du neurologue ? Et comment évolue cette « muse » des mathématiques et des sciences exactes, cette muse des sciences dures ? Ses origines sont d’abord la contemplation du « ciel étoilé au-dessus de nos têtes » (Kant), le goût de connaître la Création, mais aussi l’établissement de la comptabilité, des cadastres et plus généralement la contribution raisonnée à un ordre social, issu de « la loi morale au fond de nos cœurs ». Mi-rêveuse, mi-citoyenne, parfois mercantile, cette muse a mûri peu à peu dans sa quête de vérité : un parcours dans la beauté qu’elle rayonne sans cesse.
Quête de vérité
Il y a des mathématiques dans la beauté, il y a de la beauté dans les mathématiques
Cette recherche porte sur l’explication de la réalité. Il s’agit de la vérité du « comment ». Celle-ci est toujours à la merci d’une révision.
Les mathématiques ne sont pourtant pas qu’un outil, si fabuleux soit-il, pour aider les physiciens. Cette muse est davantage. Elle inspire l’abstraction, offre la liberté de choisir des axiomes liés à de nouveaux espaces, elle pousse à généraliser hardiment mais avec force discernement. Par la hauteur de vue qu’elle confère, et comme le faisait remarquer Poincaré, elle nous permet de donner le même nom à des êtres a priori très différents. Pure et jubilatoire activité pourtant fertile grâce à d’imprévisibles mais possibles applications techniques. Pour parvenir à ces altitudes, le mathématicien doit pratiquer « l’économie de moyens ». C’est une contrainte également bien connue des artistes.
Séduction de la beauté
Sir Michaël Atiyah rappelle qu’entre la vérité et la beauté le mathématicien est surtout séduit par la beauté, elle est immédiate et satisfait l’esprit, alors que la quête de la vérité se fait par progression et n’a jamais de fin.
Nous frôlons ici le mystère du cerveau. Ces robots présentés peuvent explorer leur milieu naturel, créer entre eux un langage commun, ils ont une curiosité artificielle au point de percevoir les effets de leurs vocalisations sur les spectateurs humains : d’où un dialogue « homme machine » amélioré. Quel bel exemple de modélisation de fonctionnement du cerveau quand il recherche du plausible à partir de données incomplètes2 !
Climat de beauté

Hiroshi Sugimoto, Conceptual Form 011, 2008. Surface de révolution présentant une courbure négative constante. Miroir en aluminium.
Dans son livre Formes et Forces (Flammarion, 1971), l’historien d’art René Huyghe exprimait sa ferme conviction que la science et l’art convergent dans leurs recherches pourtant si différentes des « articulations fondamentales du Réel ». Sensibles et créatifs, les peintres et sculpteurs utilisent des formes de base telles que les segments de droite, les angles, pentagones, cercles et cercles concentriques, spirales ou courbes périodiques. Nous retrouvons ces figures dans les Sciences, sauf dans l’infiniment petit.
Dans la matière inerte et solide, dans les cristaux par exemple, les segments et les angles prévalent ; si la matière est souple, elle prend selon ses états des formes de tourbillons, de spirales qui expriment sa plasticité face aux forces qui la pétrissent. Et quand surgit la vie, ses formes de croissance sont les tiges rectilignes, les bulbes et fruits sphériques, les spirales chères à Fibonacci, etc.
Cinquième mystère
Terminons par ce texte japonais tiré du catalogue de l’exposition : « Il y a des mathématiques dans la beauté, il y a de la beauté dans les mathématiques. » Cette beauté nous fait voyager et nous dépayse. Et si le « cinquième mystère » était la beauté ?
Arts et mathématiques
Comme le rappelle Claude Allègre dans son Dictionnaire amoureux de la science, les Grecs mettaient la musique et les mathématiques dans les beaux-arts. Les expressions et figures de ces dernières sont d’une beauté qui pousse à la contemplation : les termes « nombre d’or », « section d’or », « division harmonique » traduisent le sobre luxe et la beauté de l’écriture mathématique. Et la découverte d’une démonstration peut être aussi source d’émotion esthétique.
____________________________
1. Cf. Misha Gromov : Les déchiffreurs, voyages en Mathématiques, Belin, Paris 2008, p. 154 à 156. Cf. aussi le catalogue abrégé de l’exposition.
2. Cf. Cours de psychologie cognitive expérimentale de Stanislas Dehaene au Collège de France, 2012.
Les photos sont publiées avec l’aimable autorisation de la Fondation Cartier pour l’art contemporain, qui a organisé l’exposition Mathématiques, un dépaysement soudain, présentée du 21 octobre 2011 au 18 mars 2012

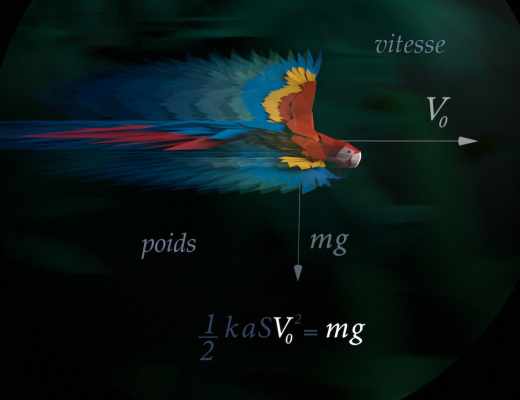


Commentaire
Ajouter un commentaire
Autre retour sur cette exposition
Un autre commentaire sur cette exposition, à lire sur mon blog de sciences : http://www.maths-et-physique.net/article-mathematiques-un-depaysement-godelien-101360709.html Et quelques remarques sur le texte ci-dessus : – GROMOV et non Gramov – par ailleurs je ne suis pas sûr que ce mathématicien ait voulu nous emmener vers des quelconques « mystères » – ce n’est pas ce que j’ai perçu dans sa bibliothèque. – Poincaré au sous-sol : ce n’étaient pas des « écrits de Poincaré » mais une remarquable fresque reliant ses divers travaux (cette fresque est reproduite pleine page dans le Bulletin B51 de la SABIX consacré au centenaire de Poincaré,que j’ai dirigé).