La modélisation mécanique en cardiologie : vers le patient virtuel

Les mal­adies car­dio­vas­cu­laires sont un prob­lème de san­té publique majeur dans le monde. Le diag­nos­tic pré­coce de ces affec­tions con­stitue un enjeu cru­cial pour assur­er leur recul. La sim­u­la­tion numérique devient petit à petit un out­il poten­tiel d’aide clin­ique, sur lequel on fonde de grands espoirs.

Le diag­nos­tic pré­coce des mal­adies car­dio-vas­cu­laires a per­mis, depuis deux décen­nies, de lim­iter sta­tis­tique­ment le développe­ment des mal­adies car­dio­vas­cu­laires face aux mal­adies can­céreuses. Cepen­dant, ce sont prin­ci­pale­ment les AVC qui ont chuté grâce à une meilleure prise en charge de l’hypertension artérielle, et dimin­uer la mor­tal­ité des autres mal­adies car­diaques reste un défi con­sid­érable mal­gré la dis­sémi­na­tion d’appareils d’imagerie de plus en plus sophis­tiqués (notam­ment l’IRM) dans les pays industrialisés.

REPÈRES

Pre­mière cause de mor­tal­ité aux États-Unis, sec­onde en Europe, les mal­adies car­dio­vas­cu­laires sont aus­si en forte crois­sance en Chine, au Brésil, comme dans de nom­breux pays émer­gents. Après les acci­dents vas­cu­laires cérébraux (AVC), les patholo­gies les plus fréquentes sont les mal­adies coro­nar­i­ennes con­duisant à l’infarctus du myocarde et à l’insuffisance car­diaque, ain­si que les trou­bles du rythme ou ary­th­mies car­diaques, mais il existe aus­si un très grand nom­bre de patholo­gies moins répan­dues, notam­ment des mal­for­ma­tions con­géni­tales. Rien qu’en Europe, ces mal­adies ont un impact économique d’environ 170 mil­liards d’euros par an. 

Le cœur, mécanique modélisable

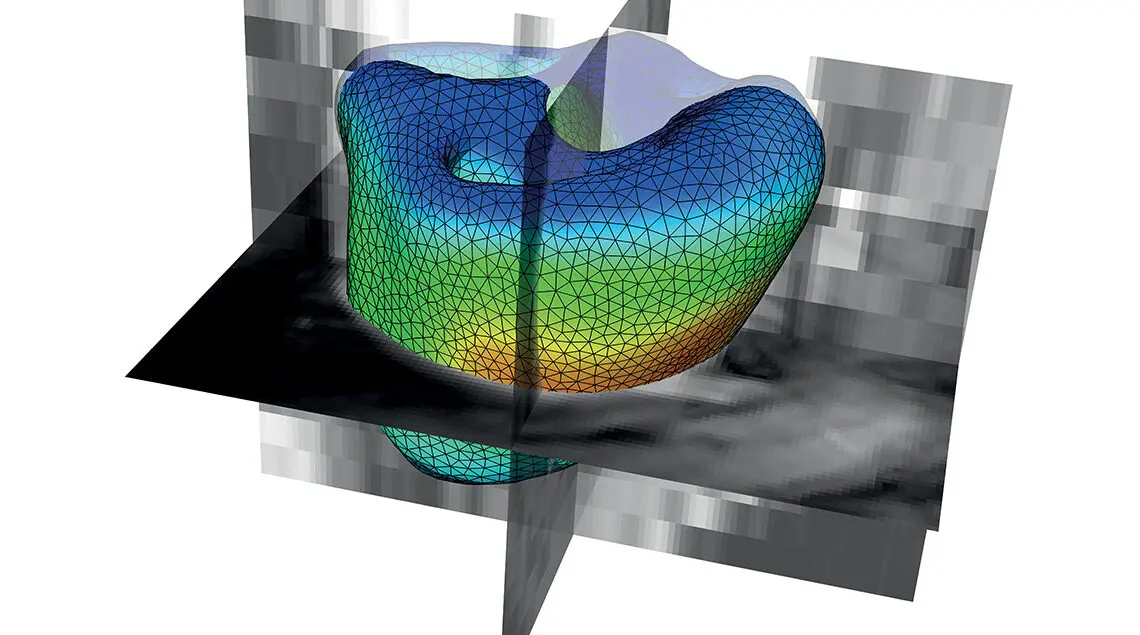
Le cœur, organe vital par excel­lence, est le siège de phénomènes physiques extrême­ment divers. À l’origine de la con­trac­tion de l’organe, on trou­ve une activ­ité élec­trique régulière, révélée à l’électrocardiogramme, cor­re­spon­dant à la prop­a­ga­tion d’une onde de dépo­lar­i­sa­tion dans le cœur. En réponse à cette acti­va­tion, le cœur se con­tracte et assure ain­si sa fonc­tion motrice : celle de pom­per le sang dans les poumons pour qu’il soit oxygéné, et vers le reste des organes pour les ali­menter. Nous ressen­tons cette activ­ité mécanique au quo­ti­di­en et on la mesure lors de l’auscultation, de la prise de ten­sion ou des exa­m­ens par imagerie médi­cale, notam­ment par échogra­phie ou IRM.

Cette richesse des phénomènes physiques éveille depuis plus d’un siè­cle la curiosité de ceux qui, comme
A. F. Hux­ley (prix Nobel de médecine 1963), souhait­ent mod­élis­er le fonc­tion­nement de l’organe au tra­vers de descrip­tions physiques et math­é­ma­tiques adap­tées, en vue d’en dégager des inter­pré­ta­tions ou appli­ca­tions pré­cis­es. Il y eut d’abord la recherche d’une com­préhen­sion en pro­fondeur des mécan­ismes tem­porels régu­lant le com­porte­ment de la cel­lule ou de la fibre car­diaque, décrites par les math­é­mati­ciens au moyen d’équations dif­féren­tielles. Mais on souhai­ta aus­si com­pren­dre, dès 1937 avec Kol­mogorov, l’évolution à la fois tem­porelle et spa­tiale de la prop­a­ga­tion de l’activité élec­trique dans l’organe ou, dans les années 50, de la con­trac­tion mécanique. Ces phénomènes dis­tribués dans l’espace sont typ­ique­ment représen­tés par des équa­tions aux dérivées par­tielles (EDP) reliant l’évolution en temps du phénomène aux vari­a­tions spa­tiales locales.

Des modèles arrivant à maturité

En par­al­lèle avec le développe­ment des out­ils de cal­cul sci­en­tifique, la com­mu­nauté mécanique s’est emparée, dès les années 70, du sujet de la mod­éli­sa­tion des phénomènes physiques à l’échelle du tis­su et de l’organe à l’aide du for­mal­isme des milieux con­ti­nus. Les mod­èles et les méth­odes com­pu­ta­tion­nelles ont pro­gres­sive­ment per­mis d’appréhender des phénomènes de plus en plus com­plex­es et de plus en plus cou­plés, de la con­trac­tion du tis­su car­diaque à son inter­ac­tion avec l’activité élec­trique ou avec le flu­ide san­guin présent dans les cav­ités cardiaques.

On peut con­sid­ér­er que cer­tains de ces mod­èles sont arrivés à matu­rité au début de la présente décen­nie, en ter­mes de capac­ité pré­dic­tive du bat­te­ment car­diaque et de cer­taines patholo­gies asso­ciées. Cela ouvrit la voie à l’utilisation de mod­èles dans le cadre du pronos­tic et du diag­nos­tic clin­ique. Ain­si, la sim­u­la­tion numérique devient petit à petit un out­il poten­tiel d’aide clin­ique, validé et encour­agé par les instances de régu­la­tion médi­cale européennes ou améri­caines par exem­ple, et porté par de nou­veaux acteurs indus­triels tels que Das­sault Sys­tèmes, qui voient ici de nou­velles appli­ca­tions de leurs out­ils de mod­éli­sa­tion numérique en ingénierie biomédicale.

Quand on par­le de pronos­tic et de diag­nos­tic assistés par l’outil numérique, il faut non seule­ment dévelop­per des mod­èles math­é­ma­tiques pré­cis et rigoureux, des méth­odes numériques robustes et effi­caces pour les simuler, mais il faut aus­si les per­son­nalis­er pour chaque patient à par­tir de don­nées bio­médi­cales (notam­ment les images issues de scan­ners, IRM, échogra­phies, etc.). Les don­nées inter­vi­en­nent de deux façons dans la per­son­nal­i­sa­tion des mod­èles : on peut, clas­sique­ment, adapter les paramètres des mod­èles pour que leurs pré­dic­tions soient au plus proche des don­nées ; on peut égale­ment ajouter des ter­mes d’écart aux don­nées directe­ment dans le modèle.

C’est l’objectif que se donne l’assimilation de don­nées, ini­tiale­ment intro­duite sur les grands sys­tèmes de météorolo­gie et cli­ma­tolo­gie, qui per­met de fusion­ner mod­èles et mesures pour pro­duire une représen­ta­tion numérique prenant en compte toutes les infor­ma­tions disponibles, c’est-à-dire les con­nais­sances a pri­ori et les mesures physiques. Il est à not­er que l’assimilation de don­nées représente aus­si une méth­ode de traite­ment de don­nées (notam­ment d’images) effi­cace, où le mod­èle cor­re­spond aux con­nais­sances a pri­ori util­isées pour régu­laris­er le prob­lème de l’extraction d’informations à par­tir des don­nées. Cette approche est d’ailleurs en légère oppo­si­tion avec le par­a­digme actuel du « tout don­nées », où des mod­èles pure­ment sta­tis­tiques sont con­stru­its unique­ment à par­tir de don­nées, sans s’appuyer sur les grands principes physiques.

“Il faut développer
des modèles mathématiques personnalisés
pour chaque patient.”

Une aide au diagnostic et au pronostic

Dans notre cas par­ti­c­uli­er de la car­di­olo­gie, en par­tant d’un bat­te­ment car­diaque virtuel pour un cœur générique sup­posé sain, nous pou­vons créer des mesures virtuelles com­pa­ra­bles à celles recueil­lies lors des exa­m­ens du patient. L’écart entre ces mesures virtuelles et les mesures réelles traduit la spé­ci­ficité du cas étudié, et les méth­odes d’assimilation de don­nées sont alors capa­bles de mod­i­fi­er le bat­te­ment car­diaque simulé en inter­pré­tant et réduisant autant que pos­si­ble cette dif­férence con­statée. Une fois la spé­ci­ficité du patient déter­minée, autrement dit le diag­nos­tic, on peut alors laiss­er évoluer la sim­u­la­tion pour réalis­er une pré­dic­tion du com­porte­ment futur, à savoir le pronos­tic. Pour ce qui est du diag­nos­tic, on peut par exem­ple, dans le cas d’un infarc­tus du myocarde, estimer de façon objec­tive et quan­ti­ta­tive la local­i­sa­tion et l’intensité du dom­mage induit dans le tissu.

En ter­mes d’aide au pronos­tic, le mod­èle per­son­nal­isé peut être util­isé pour tester in sil­i­co l’impact de divers­es straté­gies thérapeu­tiques (phar­ma­colo­gie, chirurgie, dis­posi­tifs…) afin de réalis­er une analyse risque / béné­fice, com­par­er quan­ti­ta­tive­ment les straté­gies et déter­min­er la plus adap­tée au patient con­cerné. L’entreprise améri­caine Heart­Flow, issue de l’université Stan­ford, réalise ain­si des pré­dic­tions par sim­u­la­tion numérique sur mod­èles per­son­nal­isés des effets de rétré­cisse­ments coro­nar­iens, per­me­t­tant alors de déter­min­er si une inter­ven­tion serait bénéfique.

Dans le même reg­istre, des équipes Inria (dont MΞDISIM) asso­ciées à l’hôpital Saint-Thomas de Lon­dres ont réal­isé une preuve de con­cept de l’utilité des mod­èles numériques per­son­nal­isés pour anticiper l’impact de la thérapie de resyn­chro­ni­sa­tion car­diaque (CRT), large­ment pra­tiquée (150 inter­ven­tions par an et par mil­lion d’habitants en Europe de l’Ouest), alors qu’on estime qu’elle ne présente aucun béné­fice, au résul­tat, pour plus d’un patient sur deux. Dans un tel exem­ple, la sim­u­la­tion numérique per­me­t­tra non seule­ment de lim­iter les coûts et les risques asso­ciés aux inter­ven­tions sans béné­fice, mais aus­si d’adapter et d’optimiser la procé­dure pour chaque patient, et ain­si d’en amélior­er sig­ni­fica­tive­ment le succès.

Un riche champ restant à explorer

Reste que la com­préhen­sion pro­fonde des mécan­ismes com­plex­es inter­venant dans le bat­te­ment de notre cœur est une source intariss­able de prob­lèmes nou­veaux pour la mod­éli­sa­tion mécanique et le cal­cul. L’équipe MΞDISIM tra­vaille aujourd’hui sur la for­mu­la­tion de mod­èles mul­ti­échelles et mul­ti­physiques per­me­t­tant par exem­ple la prise en compte de la per­fu­sion (ali­men­ta­tion en sang) du tis­su car­diaque et des patholo­gies asso­ciées (ischémie, infarc­tus), les phénomènes de prop­a­ga­tion d’ondes que de nou­velles tech­niques d’élastographie com­men­cent à révéler, ou encore les effets fins des grandes défor­ma­tions mécaniques sur l’activité électrique.

Aux plus grandes échelles de temps, les phénomènes de crois­sance et de remod­e­lage, qui en majeure par­tie trou­vent leurs sources aux plus petites échelles spa­tiales, sont des enjeux impor­tants, tout autant que les mécan­ismes de régu­la­tion et de cou­plage entre les dif­férents com­par­ti­ments du sys­tème car­dio­vas­cu­laire. À titre d’exemple, en col­lab­o­ra­tion avec l’université Stan­ford, l’équipe a pro­posé un mod­èle de crois­sance (évo­lu­tion de la quan­tité de matière) du myocarde qui per­met de repro­duire le remod­e­lage des ven­tricules au fil des mois et des années, notam­ment du fait de l’hypertension artérielle ou pulmonaire.

Ces avancées théoriques doivent être accom­pa­g­nées de développe­ments expéri­men­taux, eux aus­si nova­teurs et adap­tés à la com­plex­ité des tis­sus vivants, car bien sou­vent les mécan­ismes physiques eux-mêmes sont mal iden­ti­fiés. Tous ces élé­ments con­stituent autant de défis sci­en­tifiques qui se con­juguent aux enjeux clin­iques, indus­triels et sociétaux.

Retrou­vez l’ensemble du dossier : La mécanique

---

Articles similaires :

Des exosquelettes pour faire marcher ceux qui ne marchent plus Éty­molo­gie :
À pro­pos de la san­té participative EMBLEEMA Partager ses don­nées de san­té pour faire pro­gress­er la recherche Lorsque san­té et tech­nolo­gie vont de pair ! Covid-19 et dia­bète, la télémédecine en pointe à Bichat Pul­sy : Des solu­tions numériques pour les acteurs de san­té du Grand Est