Concilier pragmatisme et rigueur

Face à un pro­blème don­né, les déci­deurs sont ame­nés à s’ap­puyer sur des modé­li­sa­tions des phé­no­mènes concer­nés, alors même que les don­nées, les lois et les objec­tifs néces­saires pour construire et ali­men­ter les modèles sont enta­chés d’in­cer­ti­tudes L’in­gé­nieur qui met en oeuvre les outils mathé­ma­tiques est donc conduit à conci­lier prag­ma­tisme – faire avec les élé­ments connus – et rigueur scien­ti­fique – ne pas biai­ser les résul­tats ou leur inter­pré­ta­tion en occul­tant les limites de la modélisation.Une démarche rigou­reuse et effi­cace vise en pre­mier lieu à iden­ti­fier toutes les incer­ti­tudes en jeu, à sélec­tion­ner les outils per­met­tant d’ob­te­nir rapi­de­ment et par ité­ra­tion un fais­ceau de résul­tats exploi­tables, et enfin à pré­sen­ter ces der­niers sous une forme qui reflète leur carac­tère probabiliste.

REPÈRES
Dans l’un des articles de ce numé­ro, Pierre Funk, de l’IRSN, explique que la France a une loi d’inventaire des matières radio­ac­tives. Fort bien, cela paraît clair. Mais en réa­li­té, quelle pré­ci­sion, pour cet inventaire ?
Les matières radio­ac­tives existent dans la nature : faut-il les comptabiliser ?
Et allons-nous des­cendre au niveau de l’aiguille radio­ac­tive (ce qui exige des hommes et du maté­riel), tan­dis que les Russes oublient des sous-marins entiers ?

Un monde d’incertitudes

Les incer­ti­tudes, on peut le dire sans plai­san­te­rie, sont le cau­che­mar de l’in­gé­nieur et, au-delà, du déci­deur. L’es­prit humain est satis­fait lors­qu’il voit une situa­tion bien nette, bien car­rée, où tout est clair dans les hypo­thèses ; il ne reste qu’à cal­cu­ler, et les poly­tech­ni­ciens s’y entendent à mer­veille. Il y a là un confort intel­lec­tuel où cha­cun se plaît : n’a­voir plus que la déci­male sui­vante à cal­cu­ler, comme disaient les phy­si­ciens de la fin du XIX^e siècle. Aujourd’­hui encore, bon nombre d’or­ga­nismes scien­ti­fiques sont com­plè­te­ment per­sua­dés que les pro­grès, dans leur domaine, dans leur dis­ci­pline, passent par des cal­culs plus rapides, plus pré­cis. Ils réclament davan­tage de moyens : des ordi­na­teurs plus puis­sants, des mailleurs plus fins. Ils sont tout contents : ils pré­sentent des résul­tats, en sor­tie, avec seize chiffres signi­fi­ca­tifs, avec un pas de temps de la seconde. Et si on leur dit : mais les don­nées en entrée ne sont connues que tous les mois et avec 20 % d’in­cer­ti­tude, ils res­tent éber­lués ; cela choque leur méca­nique intel­lec­tuelle. Puis­qu’ils sont capables de four­nir, en sor­tie, des résul­tats pré­cis, il fau­drait les ali­men­ter avec des don­nées pré­cises. Pour eux, c’est la faute des expé­ri­men­ta­teurs, des four­nis­seurs de don­nées, qui n’ont pas fait leur bou­lot cor­rec­te­ment. Les ingé­nieurs ne reçoivent que des don­nées incom­plètes et incer­taines, alors qu’ils auraient méri­té mieux. À aucun moment ils ne remet­tront en cause la per­ti­nence de leur approche intel­lec­tuelle : ils res­tent per­sua­dés que c’est la socié­té qui, par manque de moyens, d’in­té­rêt, ne leur four­nit pas les ali­ments qui leur sont dus.

Trois sortes d’incertitudes

Or, les incer­ti­tudes existent néces­sai­re­ment dans toute situa­tion réelle. Il y a en réa­li­té trois sortes d’incertitudes :

• - sur les données ;
• - sur les lois ;
• - sur les objectifs.

L’in­cer­ti­tude sur les don­nées est la plus facile à com­prendre. Quand on relève un débit, une tem­pé­ra­ture, une pres­sion, chaque mesure est enta­chée d’une incer­ti­tude, et il arrive que des don­nées manquent parce que quelque chose n’a pas fonc­tion­né. L’in­cer­ti­tude sur les lois tient à notre igno­rance des lois de la nature. Le dépla­ce­ment d’une pol­lu­tion, le vieillis­se­ment d’un maté­riau, le com­por­te­ment d’un satel­lite sont autant de domaines où nous n’a­vons que des connais­sances par­tielles, approxi­ma­tives, sou­vent empi­riques. On ne peut pas pré­dire avec cer­ti­tude le moment où une pol­lu­tion attein­dra tel site, où une ampoule ces­se­ra d’é­clai­rer, où un satel­lite ren­tre­ra dans l’at­mo­sphère. L’in­cer­ti­tude sur les objec­tifs cor­res­pond à la ques­tion : que veut-on faire ? Et c’est la plus dif­fi­cile, parce qu’en géné­ral il y a plu­sieurs objec­tifs, flous et contra­dic­toires. Veut-on dimi­nuer les coûts ? à court terme ? à long terme ? aug­men­ter les com­pé­tences ? gar­der des res­sources pour l’an prochain ?

Réflé­chir d’abord
Une réflexion pré­li­mi­naire sur les trois incer­ti­tudes : don­nées, lois, objec­tifs, devrait être obli­ga­toire avant de cher­cher à résoudre un pro­blème. Mal­heu­reu­se­ment, c’est l’exception, aus­si bien dans l’approche scien­ti­fique que dans la pré­sen­ta­tion des résul­tats. On donne un scé­na­rio, avec des résul­tats pré­cis, et on « oublie » de dire que ce scé­na­rio n’est qu’un choix par­mi une infi­ni­té d’autres.
Une telle démarche induit une sus­pi­cion : ce scé­na­rio n’a‑t-il pas été choi­si pour prou­ver ce que l’on veut prou­ver, et tous les autres, qui diver­ge­raient des posi­tions atten­dues, n’ont-ils pas été éli­mi­nés d’office ?

Le recours à la modélisation n’est pas toujours pertinent

L’in­cer­ti­tude sur les lois paraît accep­table pour un esprit rationnel

L’in­cer­ti­tude sur les lois paraît accep­table pour un esprit ration­nel. Nous savons tous qu’aux hautes vitesses, il faut tenir compte d’une cor­rec­tion rela­ti­viste, négli­geable aux basses vitesses. Fort bien, et après ? Mais la ques­tion n’est pas du tout de l’ap­proxi­ma­tion des lois de la nature ; elle tient aux choix qui sont faits dans les modèles. Pre­nons un exemple amu­sant, où les mathé­ma­tiques se sont effon­drées ! Nous avons une col­la­bo­ra­tion scien­ti­fique, dans le cadre d’un pro­gramme appe­lé » Robust Mathe­ma­ti­cal Mode­ling « , avec plu­sieurs uni­ver­si­tés, dont celle de Kent (Ohio, USA). Dans le cadre de ce pro­gramme, mes amis de Kent ont reçu le res­pon­sable d’une socié­té de trans­ports (plu­sieurs cen­taines de camions) qui cher­chait à mini­mi­ser ses coûts, notam­ment d’es­sence. Comme l’es­sence, aux USA, n’a pas le même prix selon les États, cette socié­té avait mis en place, à grands frais, un logi­ciel qui rapa­triait les coûts selon les sta­tions-ser­vices et cal­cu­lait les meilleurs iti­né­raires. Cette branche des mathé­ma­tiques s’ap­pelle la » recherche opé­ra­tion­nelle « , et ce logi­ciel avait repré­sen­té un inves­tis­se­ment de plu­sieurs cen­taines de mil­liers de dol­lars. Il ne don­nait pas satis­fac­tion, et les cher­cheurs de Kent avaient été consul­tés pour l’ex­per­ti­ser : quelles variables fal­lait-il uti­li­ser, et com­ment ? Et puis le res­pon­sable de la socié­té de trans­ports s’est aper­çu qu’il avait inté­rêt à négo­cier avec les pétro­liers : si, avec mes cen­taines de camions, je prends de l’es­sence dans telle sta­tion-ser­vice, vous me consen­tez 10 % de réduc­tion. Et le logi­ciel a fini à la pou­belle, l’ex­per­tise aus­si. Sur cet exemple, on s’a­per­çoit que les lois n’é­taient pas cor­rec­te­ment connues. Les prix, à chaque sta­tion, n’au­raient pas dû être consi­dé­rés comme fixes. Mais il est impos­sible de savoir a prio­ri quelle four­chette de négo­cia­tion est possible.

Le prix, variable volatile et irrationnelle

De manière très géné­rale, on peut dire qu’il faut, si pos­sible, évi­ter de faire inter­ve­nir les prix dans un pro­blème d’op­ti­mi­sa­tion, parce qu’il s’a­git d’une variable vola­tile, irra­tion­nelle, et dont les varia­tions sont brusques et incon­trô­lables. Par exemple, si l’on cherche à pré­dire la consom­ma­tion d’éner­gie dans dix ans, il vaut mieux le faire sur la base des besoins esti­més, par sec­teur, à par­tir d’un his­to­rique : on aura une pré­vi­sion rela­ti­ve­ment robuste et fiable, tan­dis qu’une pré­vi­sion du prix du pétrole est très dif­fi­cile. Bien enten­du, dès que l’on touche à la pros­pec­tive, l’i­gno­rance sur les lois est la règle. À l’ho­ri­zon de dix ou vingt ans, on ne peut savoir avec pré­ci­sion quelle sera la popu­la­tion, quels seront les consom­ma­tions, les besoins, etc. L’at­ti­tude scien­ti­fique, répon­dant à un sou­ci d’hon­nê­te­té mini­male, consiste évi­dem­ment à men­tion­ner toutes les incer­ti­tudes pos­sibles ou à venir Ce peut être fait de diverses manières : en don­nant des inter­valles de confiance (pro­ba­bi­listes ou non) sur les dif­fé­rents para­mètres, en adop­tant des scé­na­rios » hauts » et » bas « , etc. L’hon­nê­te­té impose aus­si de dis­tin­guer entre incer­ti­tudes sur les don­nées et incer­ti­tudes sur les modèles (c’est-à-dire sur les lois qui ont été rete­nues). Cela consiste à dire : dans le cadre de ce modèle, je trouve une incer­ti­tude de 10 % en sor­tie, mais c’est parce que j’ai sup­po­sé que les varia­tions de tel para­mètre étaient linéaires entre telle et telle borne. Sans cette hypo­thèse (sou­vent fac­tice) de linéa­ri­té, mes incer­ti­tudes seraient différentes.

Gare au consensus d’experts

Confron­ter avec l’expérience
De nos jours, on entend sou­vent dire que les experts se sont mis d’accord pour déci­der que tel modèle était valide. Une telle affir­ma­tion est tota­le­ment dépour­vue de valeur scien­ti­fique : un modèle ne peut être vali­dé que par confron­ta­tion avec l’expérience, avec la réa­li­té. Par exemple, on ne peut pas « démon­trer » le réchauf­fe­ment cli­ma­tique au moyen de modèles.

Dans l’é­tat actuel des choses, et en par­ti­cu­lier dans le domaine de l’en­vi­ron­ne­ment, l’in­cer-ti-tude sur les modèles n’est presque jamais consi­dé­rée, pas même men­tion­née. Il se crée ins­tan­ta­né­ment » un consen­sus d’ex­perts « , pour uti­li­ser telle loi à tel endroit, par exemple tel équi­libre éco­no­mique entre l’offre et la demande. Un tel modèle n’est jamais vali­dé, n’est jamais confron­té à l’ex­pé­rience, mais il acquiert vite force de loi, par le consen­sus des experts, et peut ain­si ser­vir de base à des déci­sions nor­ma­tives. Je lis quel­que­fois » un modèle mathé­ma­tique a démon­tré que… « . Une telle phrase est une absur­di­té. Un modèle mathé­ma­tique n’est qu’une ten­ta­tive de repré­sen­ta­tion de la réa­li­té, plus ou moins pré­cise, plus ou moins com­plète, qu’il faut ensuite vali­der, c’est-à-dire confron­ter à l’ex­pé­rience, pour voir si le théo­ri­cien a réel­le­ment com­pris quelque chose. Pre­nez un tableau, fait par un peintre, repré­sen­tant une rivière. C’est une repré­sen­ta­tion de la réa­li­té, qui en vaut bien une autre. Mais vous ne diriez pas : ce tableau prouve que l’on peut tra­ver­ser la rivière à gué.

La réduction des incertitudes peut s’avérer ruineuse et stérile

On peut tou­jours, évi­dem­ment, réduire les incer­ti­tudes sur n’im­porte quoi, mais cela coûte des res­sources, qui pour­raient être mieux employées ailleurs. Le com­bat pour la réduc­tion à tout prix n’est pas sain, de même que le com­bat pour la pro­tec­tion à tout prix. Il faut se sou­ve­nir que, quoi qu’on fasse, sub­sis­te­ra tou­jours un niveau d’in­cer­ti­tude, et un niveau de dan­ger, et qu’ils doivent être pris en compte. L’at­ti­tude consis­tant à dire : fai­sons comme si tout était connu, et cher­chons ensuite à réduire les incer­ti­tudes n’est pas bonne dans son prin­cipe. On s’at­tend, bien sûr, à ce que la posi­tion de quelque îlot dans le Paci­fique ne soit pas connue avec une extrême pré­ci­sion. Mais on sait moins qu’il reste des endroits où les fron­tières de la France sont floues à 100 ou 200 mètres près. C’est le cas avec l’I­ta­lie, près du mont Blanc, et avec l’Es­pagne, près de l’en­clave de Lli­via (source : IGN). On voit ain­si, sur ce petit exemple, com­bien les don­nées res­tent impré­cises, même dans nos États modernes. Il en va de même sur la plu­part des sujets : reve­nus, chô­mage, durée de vie, etc. On peut tou­jours, bien sûr, amé­lio­rer cette connais­sance, mais le coût asso­cié devient vite injus­ti­fié. C’est un élé­ment très géné­ral, que les ingé­nieurs, tou­jours très car­té­siens, com­prennent mal et acceptent mal : une pré­ci­sion exces­sive est inutile. On pour­rait pas­ser du temps, consa­crer de l’argent, à amé­lio­rer le tra­cé de nos fron­tières : des­cendre au mètre, voire au mil­li­mètre. Mais à quoi bon ?

La modélisation peut éclairer la prise de décision en univers incertain à condition de respecter une démarche progressive et rigoureuse

Dès qu’on touche à la pros­pec­tive, l’ignorance des lois est la règle

Com­men­çons par une remarque de bon sens : chaque jour, cha­cun de nous est ame­né à prendre des déci­sions, sans jamais avoir toute l’in­for­ma­tion dis­po­nible : choix d’un iti­né­raire, d’un res­tau­rant, choix pro­fes­sion­nels, etc. Nous y par­ve­nons pour­tant, sou­vent par com­pa­rai­son avec des situa­tions anciennes, sou­vent par éli­mi­na­tion. Bien sûr, ces déci­sions ne sont pas » opti­males « , mais elles sont prises en un temps géné­ra­le­ment court. Autre­ment dit, le pro­ces­sus de déci­sion ne résulte pas d’un algo­rithme d’op­ti­mi­sa­tion, au sens aca­dé­mique du mot : l’in­tel­li­gence humaine ne construit pas une » fonc­tion objec­tif « , qu’elle cherche à opti­mi­ser sous cer­taines contraintes. Par­tant de cette remarque, nous avons cher­ché à amé­lio­rer les outils per­met­tant la prise de déci­sion en envi­ron­ne­ment incer­tain : c’est l’ob­jet de notre pro­gramme de recherche » Robust Mathe­ma­ti­cal Mode­ling » (en col­la­bo­ra­tion avec une soixan­taine d’ins­ti­tu­tions, entre­prises, uni­ver­si­tés), auquel j’ai déjà fait allu­sion plus haut. Les règles de base sont assez simples :

• - on ne recherche pas un opti­mum pré­cis (qui est dépour­vu de sens), mais une solu­tion accep­table obte­nue rapi­de­ment (Quick Accep­table Solu­tion, QAS). On aban­donne donc com­plè­te­ment la recherche d’un opti­mum ; il n’y a plus que des contraintes. Par exemple : faire une tour­née avec 3 % de camions en moins, par rap­port à l’an der­nier, ou 5 % de temps en moins, etc. Dès qu’une QAS est trou­vée, on peut ren­for­cer les contraintes, et si on ne trouve pas de QAS, on les relaxe ;
• - les contraintes elles-mêmes sont sim­pli­fiées, car il ne sert à rien de décrire une contrainte de manière fine dans un envi­ron­ne­ment incer­tain. On les sup­pose par exemple linéaires par morceaux ;
• - toutes les don­nées, para­mètres, lois, qui ne sont pas connus avec pré­ci­sion sont trai­tés sous forme de lois de pro­ba­bi­li­té : loi uni­forme, si on ne connaît que deux bornes, lois plus spé­ci­fiques si on dis­pose d’in­for­ma­tions particulières.

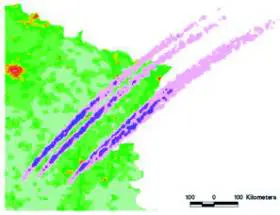
Le résul­tat est alors don­né sous forme de » carte pro­ba­bi­liste « , et non plus de résul­tat pré­cis. Voi­ci un exemple : En 2004–2005, le CNES nous avait deman­dé d’é­tu­dier les risques asso­ciés à la chute des débris pro­ve­nant de la dés­in­té­gra­tion de satel­lites. Il y a très peu de don­nées et les lois sont mal connues. En par­ti­cu­lier, dans la for­mule don­nant la résis­tance de l’air, nous avons consi­dé­ré que la den­si­té de l’air, aux dif­fé­rentes alti­tudes, était pro­ba­bi­liste ; de même pour la forme du débris, sa masse, le coef­fi­cient de traî­née, et même l’ex­po­sant de la vitesse : per­sonne n’est sûr que la résis­tance soit pro­por­tion­nelle au car­ré de la vitesse, pour des mobiles à 7 km/s en atmo­sphère raré­fiée, à 100 km d’al­ti­tude. Le résul­tat n’a pas été un point de chute pré­cis, mais une » carte pro­ba­bi­liste » : voi­ci où les débris peuvent tom­ber, avec quelle probabilité.

La recherche mathématique, correspondant aux situations incertaines, n’en est qu’à ses balbutiements

Les incer­ti­tudes existent, et elles existent de manière fondamentale

Tout reste à inven­ter. Les dif­fi­cul­tés sont scien­ti­fiques et tech­niques, mais sur­tout cultu­relles : les ingé­nieurs aiment cal­cu­ler pré­ci­sé­ment, et les experts vou­draient fon­der une déci­sion pré­cise sur une connais­sance pré­cise. C’est pour­quoi les déci­deurs, les poli­tiques, se plaignent si sou­vent des rap­ports d’ex­perts : ils leur reprochent de se réfu­gier der­rière leurs incer­ti­tudes, leurs igno­rances, pour ne pas prendre posi­tion. Ce reproche est légi­time, et je crois que les scien­ti­fiques doivent l’as­su­mer : nous devons four­nir une aide à la déci­sion, même en envi­ron­ne­ment incer­tain, car les déci­sions seront fina­le­ment prises, avec ou sans nous. C’est à nous de four­nir des outils, même impar­faits, même gros­siers, qui puissent éclai­rer ces déci­sions ; si nous ne le fai­sons pas, elles seront prises sans nous, et nous n’au­rons pas le droit de nous en plaindre. À l’in­verse, si nous éclai­rons le déci­deur, même de manière impar­faite, même de manière gros­sière, l’ex­pé­rience prouve qu’il suit géné­ra­le­ment les avis qui lui sont don­nés. Nous por­tons alors pour par­tie la res­pon­sa­bi­li­té des déci­sions qui sont prises, et c’est ce qu’il faut souhaiter.

---

Articles similaires :

Déter­mi­ner la vul­né­ra­bi­li­té des struc­tures aux séismes En matière d’énergie, il faut appri­voi­ser l’incertitude, à défaut de la domestiquer Réseaux de trans­port urbain : mieux anti­ci­per et mieux réagir Une approche pro­ba­bi­liste pour mieux gérer les mou­ve­ments de terrain La ges­tion des incertitudes