Une approche probabiliste pour mieux gérer les mouvements de terrain

Les mou­ve­ments de ter­rain, affec­tant une zone limi­tée, sont l’a­bou­tis­se­ment d’un pro­ces­sus qui peut prendre plu­sieurs mil­liers d’an­nées. Peut-on les pré­voir et sur­tout éva­luer les consé­quences des risques encou­rus ? L’emploi des pro­ba­bi­li­tés peut-il aider les spé­cia­listes ? Lorsque l’on ne dis­pose que de très peu d’in­for­ma­tions, une ana­lyse déter­mi­niste, mise en oeuvre par un expert che­vron­né, per­met en géné­ral de faire face aux incer­ti­tudes de façon satis­fai­sante. Dans les cas où l’on a col­lec­té suf­fi­sam­ment de don­nées quan­ti­ta­tives, l’ap­proche pro­ba­bi­liste, com­bi­née avec une appré­cia­tion des enjeux et de leur vul­né­ra­bi­li­té, devient un puis­sant outil d’aide à la décision.

Un évé­ne­ment « unique »
Par rap­port à d’autres phé­no­mènes natu­rels, séismes, inon­da­tions, ava­lanches, etc., les mou­ve­ments de ter­rain pré­sentent quelques spé­ci­fi­ci­tés : chaque évé­ne­ment affecte une zone limi­tée, à la dif­fé­rence par exemple d’un séisme qui frappe de vastes régions ; cer­tains évé­ne­ments sont par­fai­te­ment iden­ti­fiés à l’avance, par exemple lorsqu’il s’agit du bas­cu­le­ment d’une colonne rocheuse bien indi­vi­dua­li­sée ; d’autres en revanche ne sont pas bien loca­li­sés (chutes de pierres le long d’une falaise, par exemple) ; chaque évé­ne­ment est unique, par oppo­si­tion aux pluies extrêmes, aux crues ou aux ava­lanches qui peuvent se pro­duire qua­si­ment à l’identique plu­sieurs fois au même endroit.

L’ex­pres­sion » mou­ve­ments de ter­rain » regroupe des phé­no­mènes très variés et la ter­mi­no­lo­gie est riche : glis­se­ments, ébou­le­ments, chutes de blocs, cou­lées boueuses, fon­tis, etc., cor­res­pon­dant à dif­fé­rents méca­nismes de rup­ture, dif­fé­rents maté­riaux (argiles, roches dures, etc.), dif­fé­rentes dyna­miques, ou dif­fé­rentes dimen­sions (de quelques déci­mètres cubes à plu­sieurs cen­taines de mil­lions de mètres cubes). La demande de » pro­ba­bi­lisme » et de quan­ti­fi­ca­tion des risques est de plus en plus pres­sante, dans le domaine des mou­ve­ments de ter­rain comme pour tous les autres risques. Si l’u­ti­li­sa­tion des pro­ba­bi­li­tés en génie para­sis­mique ou en hydro­lo­gie a déjà une longue his­toire, il n’en est pas de même pour ce qui concerne les mou­ve­ments de ter­rain. Nous exa­mi­nons ci-des­sous dans quelle mesure l’emploi des pro­ba­bi­li­tés peut aider à répondre aux pre­mières ques­tions posées au spé­cia­liste : quand ? où ? quoi ? Selon la ter­mi­no­lo­gie habi­tuelle des risques natu­rels, le terme d’a­léa désigne l’oc­cur­rence du phé­no­mène natu­rel, le terme de risque incluant les consé­quences sur les per­sonnes et sur les biens.

Le déclenchement d’un mouvement de terrain

Ébou­le­ments en Lozère.

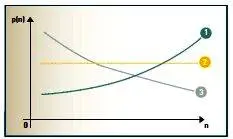Figure 1 – Évo­lu­tions des pro­ba­bi­li­tés de rup­ture durant l’année n, condi­tion­nel­le­ment à la sur­vie jusqu’à l’année n‑1.

Un mou­ve­ment de ter­rain d’o­ri­gine natu­relle est l’a­bou­tis­se­ment d’un pro­ces­sus de pré­pa­ra­tion et de déve­lop­pe­ment de la rup­ture qui peut prendre plu­sieurs décen­nies, plu­sieurs siècles ou plu­sieurs mil­liers d’an­nées. Les mou­ve­ments de ter­rain consti­tuent en effet un des méca­nismes de l’é­ro­sion qui assure le déman­tè­le­ment pro­gres­sif des reliefs. En ce sens, on peut consi­dé­rer que la mise en mou­ve­ment, en un point don­né d’un ver­sant, de tranches suc­ces­sives de ter­rain (à l’é­chelle du temps géo­lo­gique), sous forme de glis­se­ments de sol meuble ou d’é­bou­le­ments rocheux, se pro­duit sui­vant un pro­ces­sus de renou­vel­le­ment : les dates d’oc­cur­rence se répar­tissent sui­vant un modèle aléa­toire ana­logue à celui uti­li­sé pour les pannes de lampes élec­triques par exemple, chaque occur­rence » rame­nant le comp­teur à zéro « . En effet, le départ d’une por­tion de ter­rain met à nu une nou­velle sur­face, qui va pro­gres­si­ve­ment être dégra­dée (alté­ra­tion météo­rique, fatigue méca­nique, éro­sion de pied par un cours d’eau, etc.) jus­qu’à ce qu’une nou­velle rup­ture se pro­duise, et ain­si de suite. Dans ce type de modèle, le » temps d’at­tente avant rup­ture » que l’on peut esti­mer (aujourd’­hui et pour un point pré­cis du ver­sant) dépend du stade de mûris­se­ment du pro­ces­sus de dégra­da­tion de ce point. Un cas par­ti­cu­lier de pro­ces­sus de renou­vel­le­ment est le pro­ces­sus de Pois­son, qui est un pro­ces­sus sans mémoire : dans ce cas, il n’y a pas de dégra­da­tion pro­gres­sive de la situa­tion, et celle-ci n’est pas influen­cée par le fait que la pré­cé­dente rup­ture soit très ancienne ou toute récente. On voit immé­dia­te­ment que ce modèle, fré­quem­ment employé pour les évé­ne­ments d’o­ri­gine météo­ro­lo­gique (l’ab­sence de mémoire d’une année sur l’autre est le plus sou­vent admis­sible), n’est pas bien adap­té aux mou­ve­ments de ter­rain. Si l’on appelle p(n) la pro­ba­bi­li­té que la rup­ture d’une masse rocheuse bien iden­ti­fiée se pro­duise durant l’an­née n, condi­tion­nel­le­ment à sa sur­vie jus­qu’au 1^er jan­vier de cette année n, on peut avoir plu­sieurs types d’é­vo­lu­tion de p(n) avec n, comme l’in­dique la figure 1. La courbe 1 repré­sente un pro­ces­sus avec dégra­da­tion pro­gres­sive : éro­sion du pied d’un ver­sant instable (pré­pa­ra­tion d’un glis­se­ment), dis­so­lu­tion d’un niveau gyp­seux (pré­pa­ra­tion d’un effon­dre­ment), etc. La courbe 2 repré­sente un pro­ces­sus de Pois­son. La courbe 3 sché­ma­tise le cas d’un site où une pro­tec­tion à effet dif­fé­ré a été mise en place, plan­ta­tion d’arbres sur un ver­sant, par exemple. Les notions cou­ram­ment employées de » pro­ba­bi­li­té annuelle » ou de » fré­quence annuelle » de rup­ture, impli­ci­te­ment consi­dé­rées comme constantes, n’ont donc de sens que dans le cas du pro­ces­sus de Pois­son. Du point de vue de la ges­tion du risque, les évo­lu­tions de type 1 et 2 sont bien dif­fé­rentes. Pre­nons par exemple une courbe de type 1 : la pro­ba­bi­li­té de rup­ture dans les dix pro­chaines années peut être consi­dé­rée comme assez faible, compte tenu de l’ab­sence d’in­dices d’é­vo­lu­tion actuelle (on n’ob­serve pas de traces fraîches de fis­sures) ; mais la pro­ba­bi­li­té de rup­ture à long terme, d’i­ci un siècle, peut être rela­ti­ve­ment éle­vée, compte tenu de la pré­sence d’un fac­teur évo­lu­tif défa­vo­rable tel qu’un banc rocheux gélif s’é­ro­dant petit à petit à la base de l’é­caille rocheuse consi­dé­rée. On peut donc accep­ter sur le site cer­tains types d’ac­ti­vi­tés ou d’ins­tal­la­tions, à carac­tère pro­vi­soire, mais on s’in­ter­di­ra tout amé­na­ge­ment lourd à durée de vie longue.

Les mouvements de terrain à l’échelle d’une zone homogène

L’exemple de La Réunion
La route natio­nale n° 1, à La Réunion, longe sur une dizaine de kilo­mètres le pied d’une falaise consti­tuée de cou­lées de basalte alter­nant avec des sco­ries très éro­dables. La Direc­tion dépar­te­men­tale de l’équipement (DDE) ayant ins­tau­ré une patrouille per­ma­nente pour le rele­vé des chutes de blocs, nous dis­po­sons de don­nées quo­ti­diennes : la fré­quence annuelle est d’environ 100 chutes pour l’ensemble de l’itinéraire. Que peut-on en déduire pour un point don­né de l’itinéraire ? La falaise pos­sé­dant une hau­teur moyenne de 60 m, la sur­face de paroi est d’environ 600 000 m². Si l’on sup­pose qu’un site d’éboulement typique repré­sente envi­ron 6 m² de falaise, et que la paroi est glo­ba­le­ment homo­gène, l’ordre de gran­deur de la période de retour en un site ponc­tuel est de mille ans.

La situa­tion est dif­fé­rente si l’on consi­dère l’oc­cur­rence d’é­vé­ne­ments non plus en un point don­né, mais sur tout un sec­teur homo­gène : cas de chutes de blocs pro­ve­nant d’un linéaire impor­tant de falaise, de fon­tis appa­rais­sant dans un pla­teau kars­tique de plu­sieurs kilo­mètres car­rés, etc. Le carac­tère homo­gène du sec­teur est essen­tiel : même for­ma­tion géo­lo­gique, mêmes condi­tions de relief, même cli­mat, etc. La série tem­po­relle des évé­ne­ments sur­ve­nant dans un tel sec­teur peut sou­vent être assi­mi­lée à un pro­ces­sus de Pois­son. Dans la mesure où le sec­teur consi­dé­ré com­prend un grand nombre de sites poten­tiels et où ces dif­fé­rents sites sont à des stades d’é­vo­lu­tion très variables, l’oc­cur­rence des évé­ne­ments devient sta­tion­naire et l’on peut par­ler alors de la période de retour T de l’é­vé­ne­ment » chute d’un bloc pro­ve­nant d’un point quel­conque de la falaise » par exemple. En moyenne, il tombe donc 1/T bloc(s) par an, si T est expri­mée en années. Il faut donc bien dis­tin­guer le diag­nos­tic en un point pré­cis, pour lequel il est indis­pen­sable d’é­va­luer le stade de déve­lop­pe­ment actuel de la rup­ture, et le diag­nos­tic à l’é­chelle régio­nale, pour lequel une approche glo­bale de type pois­so­nien peut suf­fire (fré­quence annuelle des événements).

L’influence des précipitations

Un modèle pro­ba­bi­liste n’a de sens que s’il est pos­sible d’estimer cor­rec­te­ment les para­mètres du modèle

L’ex­pé­rience montre que les insta­bi­li­tés se pro­duisent essen­tiel­le­ment pen­dant la sai­son plu­vieuse ou à la fonte des neiges. La dépen­dance vis-à-vis des pré­ci­pi­ta­tions conduit à envi­sa­ger une pro­ba­bi­li­té de l’é­vé­ne­ment condi­tion­nel­le­ment à une pré­ci­pi­ta­tion don­née, par exemple cumu­lée sur les der­nières 24 heures ; cette approche a été uti­li­sée à une échelle régio­nale dans une pers­pec­tive d’a­lerte à court terme, à Hong-Kong notam­ment. Sur la RN 1 de La Réunion, il est patent que les chutes de blocs sont très nom­breuses lors des fortes pluies tro­pi­cales. L’é­tude sta­tis­tique montre que le nombre men­suel N de chutes de blocs peut être relié à la hau­teur men­suelle de pré­ci­pi­ta­tions, la cor­ré­la­tion res­tant tou­te­fois médiocre. Tou­te­fois, comme on le ver­ra plus loin, la dépen­dance vis-à-vis de la pluie, pour limi­tée qu’elle soit, peut être exploi­tée pour amé­lio­rer la ges­tion du risque à court terme.

La difficulté de l’estimation

L’u­ti­li­sa­tion d’un modèle pro­ba­bi­liste n’a de sens que s’il est pos­sible d’es­ti­mer cor­rec­te­ment les para­mètres du modèle. De façon géné­rale, on dis­pose de deux types de méthodes pour iden­ti­fier une pro­ba­bi­li­té : les méthodes indi­rectes et les méthodes directes.

Des cal­culs complexes
En pra­tique, l’emploi des méthodes indi­rectes est frei­né par la com­plexi­té des cal­culs, si l’on veut prendre en compte la varia­bi­li­té spa­tiale des carac­té­ris­tiques méca­niques ou les cor­ré­la­tions entre celles-ci, et sur­tout par l’importance des recon­nais­sances géo­tech­niques qu’il serait néces­saire d’entreprendre pour pou­voir esti­mer cor­rec­te­ment les paramètres.
En outre, la plu­part des auteurs qui ont expé­ri­men­té cette approche n’ont pas incor­po­ré, dans leur modèle pro­ba­bi­liste, le temps, qui inter­vient à tra­vers les varia­tions de la hau­teur des nappes phréa­tiques ou le « vieillis­se­ment » des carac­té­ris­tiques mécaniques.

Les méthodes indi­rectes sont sou­vent uti­li­sées dans le risque indus­triel : la pro­ba­bi­li­té de ruine du sys­tème est éva­luée à par­tir des pro­ba­bi­li­tés de rup­ture des dif­fé­rents élé­ments qui com­posent le sys­tème, ou en fonc­tion de carac­té­ris­tiques dont les lois de pro­ba­bi­li­té sont elles-mêmes connues. Dans le domaine des insta­bi­li­tés de pente, on peut ten­ter d’é­va­luer : Pro­ba (insta­bi­li­té) = Pro­ba (F = R/M <1) où F repré­sente le coef­fi­cient de sécu­ri­té, R les efforts résis­tants maxi­maux mobi­li­sables et M les efforts moteurs. R et M sont consi­dé­rés comme des fonc­tions de variables aléa­toires telles que les résis­tances au cisaille­ment des sols ou l’é­pais­seur des ter­rains meubles. Les méthodes directes d’es­ti­ma­tion reposent sur la fré­quence empi­rique des évé­ne­ments. L’hy­po­thèse impli­cite est que les condi­tions géné­rales futures seront les mêmes que par le pas­sé ; elle est en géné­ral jus­ti­fiée pour les phé­no­mènes tels que les mou­ve­ments de ter­rain, même si les chan­ge­ments cli­ma­tiques peuvent per­tur­ber l’a­na­lyse sur de très longues durées. Dans le cas des inon­da­tions ou des pluies extrêmes par exemple, on dis­pose de séries his­to­riques de don­nées qui per­mettent d’es­ti­mer des périodes de retour décen­nales ou cen­ten­nales satis­fai­santes. En ce qui concerne les mou­ve­ments de ter­rain, il est très rare de dis­po­ser de don­nées suf­fi­santes, le cas de la RN 1 cité plus haut res­tant exceptionnel.

La question de l’intensité

C’est une obser­va­tion de por­tée géné­rale que les phé­no­mènes de grande ampleur sont (heu­reu­se­ment) moins fré­quents que ceux de faible ampleur, qu’il s’a­gisse de chutes de météo­rites, de séismes, de crues tor­ren­tielles ou de mou­ve­ments de terrain.

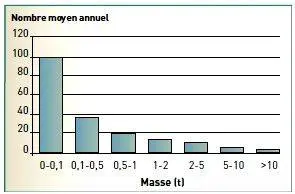
Figure 2 – His­to­gramme des chutes de blocs sur la RN 1, selon la masse éboulée.

En géné­ral, le contexte mor­pho­lo­gique et géo­lo­gique per­met de don­ner une dimen­sion maxi­male aux mou­ve­ments de ter­rain pou­vant se pro­duire sur un site don­né : pour un glis­se­ment de ter­rain par exemple, la lon­gueur de la pente, l’é­pais­seur des for­ma­tions super­fi­cielles mobi­li­sables, etc. Les don­nées sta­tis­tiques dis­po­nibles pour les évé­ne­ments de grande ampleur, donc rares, sont insuf­fi­santes pour caler cor­rec­te­ment un modèle pro­ba­bi­liste. On a recours alors le plus sou­vent à une extra­po­la­tion à par­tir des petites inten­si­tés : dans le cas des crues et des séismes, diverses méthodes ont été mises au point. Qu’en est-il pour les mou­ve­ments de ter­rain ? On peut admettre qu’une extra­po­la­tion est valable tant que les phé­no­mènes répondent aux mêmes méca­nismes et aux mêmes causes. Sur la RN 1 à La Réunion par exemple, la décrois­sance de la fré­quence selon la masse ébou­lée est mani­feste (figure2), mais les phé­no­mènes majeurs s’a­na­lysent comme l’é­bou­le­ment d’une tranche de falaise ayant une épais­seur de plu­sieurs mètres, avec une lar­geur et une hau­teur de quelques dizaines de mètres, c’est-à-dire un méca­nisme très dif­fé­rent des chutes de blocs cou­rantes liées à la mise en dés­équi­libre d’un niveau de cou­lée basal­tique repo­sant sur des sco­ries éro­dables : il n’y a donc pas de rai­son objec­tive d’ex­tra­po­ler les fré­quences de la figure 2 à ces ébou­le­ments majeurs.

La tra­jec­to­gra­phie
La tra­jec­toire d’un bloc déva­lant une pente par une suc­ces­sion de rebonds désor­don­nés est impos­sible à pré­voir pré­ci­sé­ment. Il paraît donc natu­rel de pré­sen­ter les résul­tats des études tra­jec­to­gra­phiques sous forme probabiliste.
La pro­ba­bi­li­té qui inté­resse le déci­deur est la com­po­sée de la pro­ba­bi­li­té de départ d’un bloc et de la pro­ba­bi­li­té que la tra­jec­toire atteigne un objec­tif, ponc­tuel ou linéaire, don­né. Concen­trons-nous sur la seconde probabilité.
L’incertitude majeure réside au niveau du rebond des blocs : la vitesse réflé­chie dépend de la vitesse inci­dente (en trans­la­tion et en rota­tion), de la masse et de la forme du bloc, de son orien­ta­tion au moment du choc et de la nature et de la pente du terrain.
La dif­fi­cul­té pro­vient du fait qu’il n’y a pra­ti­que­ment aucune don­née expé­ri­men­tale per­met­tant de construire des dis­tri­bu­tions de pro­ba­bi­li­té four­nis­sant l’angle de réflexion ou la vitesse réflé­chie lors d’un rebond… Il est donc indis­pen­sable – mais c’est rare­ment fait – de véri­fier la robus­tesse des résul­tats par rap­port aux dis­tri­bu­tions de pro­ba­bi­li­té initiales.

La gestion du risque à l’aide de l’approche probabiliste

Le ges­tion­naire d’un ouvrage mena­cé ou le maire d’une com­mune inquiet pour la sécu­ri­té des habi­tants ont à prendre des déci­sions telles que : inves­tis­se­ment dans un ouvrage de pro­tec­tion, éva­cua­tion d’une mai­son, etc. Ce n’est pas seule­ment l’a­léa, qui concerne uni­que­ment le phé­no­mène natu­rel, mais plu­tôt le risque, pre­nant en compte les consé­quences, qui inté­resse les décideurs.

C’est le risque, pre­nant en compte les consé­quences, qui inté­resse les décideurs

Dans le cas d’une route située en pied de falaise par exemple, l’ac­ci­dent se pro­duit si un bloc atteint la route au moment du pas­sage d’un véhi­cule, conjonc­tion heu­reu­se­ment beau­coup moins pro­bable que la seule chute (il fau­drait aus­si ana­ly­ser la pos­si­bi­li­té d’ac­ci­dent lié à la pré­sence d’un bloc tom­bé peu avant le pas­sage d’un véhi­cule). Pour un aléa don­né, le risque de » coup au but » sera d’au­tant plus éle­vé que le temps de séjour des véhi­cules dans la zone expo­sée sera long ; ce temps d’ex­po­si­tion est une fonc­tion du tra­fic et de la flui­di­té de la cir­cu­la­tion. Dans un pre­mier temps, à sup­po­ser que l’on sache esti­mer le risque cor­rec­te­ment, celui-ci est com­pa­ré au risque consi­dé­ré comme accep­table. De façon géné­rale, celui-ci peut s’ex­pri­mer sous la forme d’un nombre moyen annuel de vic­times, ou d’un coût moyen annuel des dom­mages. Si le risque est consi­dé­ré comme inac­cep­table, il faut alors mettre en balance d’une part le coût (éco­no­mique, social, envi­ron­ne­men­tal) des diverses mesures de pré­ven­tion, et d’autre part les risques rési­duels cor­res­pon­dants. La mise en sécu­ri­té abso­lue étant rare­ment pos­sible, une stra­té­gie de pro­tec­tion doit être choi­sie en évi­tant deux types d’ex­cès : l’ex­cès d’op­ti­misme, lais­sant une trop grande pos­si­bi­li­té d’ac­ci­dent, et l’ex­cès de pes­si­misme, entraî­nant des coûts injus­ti­fiés pour la col­lec­ti­vi­té (sur­pro­tec­tion).

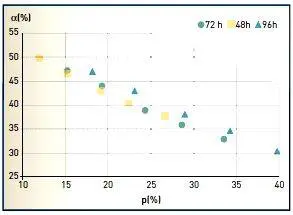
Figure 3- Repré­sen­ta­tion gra­phique des dif­fé­rentes stra­té­gies de fer­me­ture de la RN 1 à La Réunion : chaque point cor­res­pond à une stra­té­gie défi­nie par un seuil de pluie S (5 – 10 – 15 -… mm/jour) et une durée de fer­me­ture D (indi­quée dans la légende).

Dans le cas de la RN 1 à La Réunion, un mode de ges­tion du risque à court terme, tenant compte de la rela­tion sta­tis­tique entre pluies intenses et chutes de blocs, a été défi­ni de la façon sui­vante (figure 3) : dès qu’un seuil S de pluie tom­bée en 24 heures est dépas­sé, la chaus­sée côté falaise, de loin la plus expo­sée, est fer­mée pen­dant une durée D (bien enten­du pro­lon­gée si le seuil est de nou­veau dépas­sé). Les don­nées sta­tis­tiques sur le site étant nom­breuses et repré­sen­ta­tives, une opti­mi­sa­tion de cette stra­té­gie de pré­ven­tion a pu être effec­tuée, en cher­chant à mini­mi­ser deux critères :

• - un cri­tère sur l’a­léa rési­duel, éva­lué par la pro­por­tion a de chutes qui sur­viennent alors que la route est ouverte au trafic,
• - un cri­tère sur le coût (l’im­pact socio-éco­no­mique de la fer­me­ture par­tielle de la route est très impor­tant), mesu­ré à l’aide de la pro­por­tion p de jours de fermeture.

Plus le seuil plu­vio­mé­trique S est bas, plus l’a­léa rési­duel (a) est impor­tant et plus p est faible ; plus la durée de fer­me­ture D est longue, plus a est faible et plus l’im­pact éco­no­mique ℗ est grand. Les points de la figure 3 repré­sentent diverses stra­té­gies de fer­me­ture (couples S, D) dans le dia­gramme (a, p). Les stra­té­gies opti­males se situent en pre­mière approxi­ma­tion sur la courbe bleue ; les points situés au-des­sus repré­sentent des stra­té­gies qui sont amé­lio­rables. Deux stra­té­gies dont les points sont situés sur la courbe ne sont pas com­pa­rables pour les cri­tères rete­nus : il revient au poli­tique de déci­der in fine de la stra­té­gie, à choi­sir par­mi l’en­semble des stra­té­gies opti­males (une autre stra­té­gie – celle qui est aus­si mise en oeuvre pro­gres­si­ve­ment – est de mettre en place des protections).

Mieux comprendre les mécanismes

Sui­vant une remarque de G. Mathe­ron, nous pou­vons rap­pe­ler que » Il n’y a pas de pro­ba­bi­li­tés en soi, il n’y a que des modèles pro­ba­bi­listes » : la pro­ba­bi­li­té est construite dans le cadre d’in­for­ma­tions connues à une cer­taine date par un indi­vi­du pour modé­li­ser la part d’in­con­nu sub­sis­tant, et sera d’au­tant plus fiable que ces infor­ma­tions seront nom­breuses et de qua­li­té (l’es­ti­ma­tion de la pro­ba­bi­li­té de glis­se­ment par le géo­tech­ni­cien n’est évi­dem­ment pas la même avant et après les forages de recon­nais­sance). Lorsque l’on ne dis­pose que de très peu d’in­for­ma­tions sur un site, ce qui est le cas le plus cou­rant, on peut pré­fé­rer à l’ou­til pro­ba­bi­liste une ana­lyse déter­mi­niste mise en oeuvre par un expert che­vron­né et inté­grant toutes les obser­va­tions de ter­rain. Une éva­lua­tion de la sen­si­bi­li­té des résul­tats aux prin­ci­paux fac­teurs per­met en géné­ral de faire face aux incer­ti­tudes de façon satis­fai­sante (Londe, 1998). Tou­te­fois, dans les (très rares) cas où l’on a col­lec­té suf­fi­sam­ment de don­nées quan­ti­ta­tives, l’ap­proche pro­ba­bi­liste, com­bi­née avec une appré­cia­tion des enjeux et de leur vul­né­ra­bi­li­té, devient un puis­sant outil d’aide à la déci­sion, en per­met­tant d’af­fec­ter un » poids » à dif­fé­rents scé­na­rios d’é­vo­lu­tion du phé­no­mène, à dif­fé­rentes stra­té­gies de pro­tec­tion, etc., le rai­son­ne­ment pro­ba­bi­liste pré­sen­tant en tout état de cause un indé­niable inté­rêt sur un plan péda­go­gique. Dans le court terme, un pro­grès signi­fi­ca­tif dans la ges­tion et la maî­trise des risques de mou­ve­ments de ter­rain vien­dront essen­tiel­le­ment, à notre avis, d’une meilleure com­pré­hen­sion des méca­nismes d’é­vo­lu­tion de ces phénomènes.

---

Articles similaires :

Conci­lier prag­ma­tisme et rigueur Le futur comme déter­mi­nant du présent : La maî­trise des incer­ti­tudes dans la défense exige une pros­pec­tive à long terme Réseaux de trans­port urbain : mieux anti­ci­per et mieux réagir La ges­tion des incertitudes