So-grid : observer et surveiller les réseaux électriques

Le projet SO-grid fut conçu et développé pour tester le contrôle d’un réseau de distribution électrique moderne, intégrant des sources d’énergie renouvelable entre autres par le biais d’une communication « Courant porteur en ligne ». Le projet donna lieu à la conception de nouveaux outils de mesure (capteurs), protocoles de communication, et méthodes innovantes pour la planification du déploiement de capteurs dans un réseau existant.

Les grands acteurs des mar­chés élec­triques inves­tissent de plus en plus dans l’adéquation de leurs réseaux de trans­port et de dis­tri­bu­tion. En France, par exemple, EDF, Ene­dis (ex-ERDF) et RTE sub­ventionnent plu­sieurs actions de recherche en mathé­ma­tiques appli­quées, infor­ma­tique et ingé­nie­rie (par exemple grâce à l’initiative PGMO ­www.fondation-hadamard.fr/PGMO). La dif­fé­rence des besoins par rap­port au pas­sé est que l’approvisionnement et la demande de puis­sance sont deve­nus moins pré­vi­sibles et cen­tra­li­sés, et ce à cause, entre autres, des sources d’énergie renou­ve­lable. Dans un scé­na­rio cen­tra­li­sé, les quelques pics de demande sont d’habitude assez bien gérés par la capa­ci­té rési­duelle du réseau, ce qui devient de plus en plus dif­fi­cile aujourd’hui, avec des consé­quences catas­tro­phiques. La ges­tion d’un réseau élec­trique est une tâche dif­fi­cile. La modé­li­sa­tion des élé­ments du réseau uti­li­sée aujourd’hui par des outils de pla­ni­fi­ca­tion fait des approxi­ma­tions par­fois gros­sières par rap­port à la réa­li­té phy­sique (une approche pré­cise mène­rait à des pro­blèmes trop dif­fi­ciles à résoudre). Pire, il ne semble pas y avoir une stan­dar­di­sa­tion com­mune et accep­tée des approxi­ma­tions de modélisation.

Par exemple, consi­dé­rons un des pro­blèmes fon­da­teurs de la dis­tri­bu­tion de l’électricité : l’Alter­na­ting Cur­rent Opti­mal Power Flow (ACOPF). Le cou­rant élec­trique oscille dans les câbles de 50 à 60 fois par seconde. Dans les équa­tions de l’ACOPF, par ailleurs, le cou­rant est modé­li­sé plu­tôt comme un liquide qui passe dans des paires de tuyaux paral­lèles, dans les deux direc­tions oppo­sées. Dans ce cas, nous uti­li­sons la moyenne comme approxi­ma­tion [1]. Nous n’approximons pas tout, évi­dem­ment : d’autres pro­prié­tés du cou­rant alter­na­tif sont bien repré­sen­tées dans le modèle.

REPÈRES

Dix par­te­naires indus­triels et aca­dé­miques ont par­ti­ci­pé au pro­jet SO-Grid lan­cé en 2013. L’École poly­tech­nique fut impli­quée dans la concep­tion des pro­to­coles de com­mu­ni­ca­tion sur les lignes de trans­port de puis­sance et le déploie­ment opti­mal des cap­teurs sur le réseau. Les acti­vi­tés de recherche ont été menées par des pro­fes­seurs et cher­cheurs du labo­ra­toire d’informatique (LIX), coau­teurs de cet article.

Le réseau intelligent, nouveau mode de transport électrique

Au début des années 2000, un nou­veau type de trans­port élec­trique fut conçu : le réseau intel­li­gent (smart grid) [2, 5]. Un tel réseau devrait : (a) éli­mi­ner la pos­si­bi­li­té des cou­pures élec­triques (bla­ckout) à large échelle engen­drées par des pannes ponc­tuelles ; (b) inté­grer la géné­ra­tion de puis­sance à par­tir de sources d’énergie renou­ve­lable ; © pré­dire et réagir aux chan­ge­ments impré­vus de demande de puis­sance ; (d) pou­voir chan­ger d’échelle en cas d’augmentation du nombre d’utilisateurs du réseau ; et (e) être doté d’outils de prise de déci­sion suf­fi­sam­ment sophis­ti­qués pour pou­voir éva­luer le prix uni­taire de puis­sance cor­rec­te­ment et de manière trans­pa­rente. Ce réseau devrait aus­si pou­voir fonc­tion­ner de manière for­te­ment (voir com­plè­te­ment) auto­ma­ti­sée, dis­po­ser d’une infra­struc­ture de com­mu­ni­ca­tion très avan­cée, et savoir se défendre des attaques cyber­né­tiques. Tou­te­fois, il est impos­sible de chan­ger un réseau exis­tant en smart grid sans une phase de tests très longue et pous­sée : c’est la véri­table moti­va­tion du pro­jet SO-grid. Une zone proche de Tou­louse fut choi­sie pour un test de trans­for­ma­tion du réseau exis­tant en smart grid, avec une atten­tion par­ti­cu­lière por­tée au contrôle, à la récolte et à la trans­mis­sion des données.

Tester un système de surveillance

Plus pré­ci­sé­ment, le pro­jet SO-grid fut démar­ré pour tes­ter un sys­tème de sur­veillance (moni­to­ring), col­lec­ter et ana­ly­ser des don­nées du réseau, dont la com­mu­ni­ca­tion repose sur la tech­no­lo­gie CPL. Au lieu de déployer un réseau de com­mu­ni­ca­tion paral­lèle au réseau de dis­tri­bu­tion (solu­tion coû­teuse), ou d’utiliser des moda­li­tés de com­mu­ni­ca­tion sans fil (GPRS, Edge, 3G/4G) (solu­tion non sécu­ri­sée), la com­mu­ni­ca­tion CPL com­bine les fré­quences de dis­tri­bu­tion avec celles de com­mu­ni­ca­tion sur les mêmes câbles. Ces fré­quences étant très dif­fé­rentes, nous pou­vons les dis­tin­guer en uti­li­sant l’analyse de Fourier.

Dans le reste de cet article, nous allons nous concen­trer sur une tâche par­ti­cu­lière que nous avons menée au sein du pro­jet SO-grid : le pla­ce­ment opti­mal des cap­teurs dans un réseau élec­trique. Pour des rai­sons de vul­ga­ri­sa­tion, nous avons fait abs­trac­tion de cer­tains détails tech­niques qui sont expli­qués en pro­fon­deur dans deux articles scien­ti­fiques [3, 4].

Méthodes mathématiques

La science des déci­sions est une dis­ci­pline à la fron­tière des mathé­ma­tiques appli­quées, de l’informatique et de l’ingénierie. Une branche de cette science, qui s’appelle recherche opé­ra­tion­nelle (RO), s’occupe du déve­lop­pe­ment des modèles mathé­ma­tiques pour la prise auto­ma­tique de déci­sions à par­tir d’une suite de don­nées d’entrée. Les modèles de la RO consistent en un objec­tif (à mini­mi­ser ou maxi­mi­ser) et en un ensemble de contraintes (à satis­faire), qui limitent l’extension des opti­ma de la fonc­tion de coût. Les fonc­tions mathé­ma­tiques impli­quées dans l’objectif et les contraintes sont expri­mées en fonc­tion de cer­taines variables appe­lées variables de déci­sion. Nous uti­li­sons des algo­rithmes pour iden­ti­fier, dans l’ensemble de toutes les valeurs des variables de déci­sion qui satis­font les contraintes, celles qui opti­misent l’objectif. En termes de nota­tion mathé­ma­tique, nous avons :

opt{f(x) | quel que soit i ≤ m g_i(x) ≤ 0} (1)

L’opérateur opt peut être soit « min » ou « max » selon la direc­tion d’optimisation de la fonc­tion objec­tive, qui est f(x). Les variables de déci­sion sont repré­sen­tées par le vec­teur x = (x₁, …, x_n). Le reste de la phrase for­melle en Éq. (1) signi­fie que « pour tous les indices i plus petits que m nous impo­sons les contraintes que les fonc­tions g_i(x) atteignent une valeur non-positive ».
En résu­mé : les dimen­sions du pro­blème sont don­nées (nous pre­nons n déci­sions assu­jet­ties à m contraintes), et nous cher­chons à affec­ter des valeurs à x telles que g_i(x) ≤ 0 pour tout i ≤ m, et f(x) est opti­mi­sée. L’Éq. (1) s’appelle une for­mu­la­tion de pro­gram­ma­tion mathé­ma­tique. Nous pou­vons trans­for­mer la grande majo­ri­té des pro­blèmes de déci­sion inté­res­sants en pra­tique et les repré­sen­ter sous la forme de l’Éq. (1). Une fois for­mu­lé, le pro­blème doit être réso­lu. Nous cher­chons des solu­tions par l’utilisation de cer­tains algo­rithmes appe­lés sol­veurs. L’efficacité et la pré­ci­sion des sol­veurs dépendent de plu­sieurs fac­teurs dont le prin­ci­pal est la linéa­ri­té ou la non-linéa­ri­té des fonc­tions f(x) et g_i(x) pour tout i ≤ m. Un autre fac­teur déter­mi­nant est la taille du pro­blème (n, m, ain­si que la lon­gueur des des­crip­tions des fonctions).

Formalisation du problème

Le pro­blème à résoudre dans le cadre du pro­jet SO-grid est le sui­vant : étant don­né un réseau, où fau­drait-il pla­cer les cap­teurs afin de pou­voir mesu­rer la ten­sion et le cou­rant dans tout le réseau, et de telle sorte que le nombre de cap­teurs soit le plus petit pos­sible ? La fonc­tion de coût est donc le nombre de cap­teurs, et la contrainte est que ce nombre réduit de cap­teurs doit pou­voir assu­rer l’observabilité de la ten­sion en tout nœud et du cou­rant sur chaque lien du réseau. Le pre­mier pas a été de pro­po­ser une for­ma­li­sa­tion mathé­ma­tique de ce pro­blème, selon les prin­cipes énon­cés. Nous avons modé­li­sé le réseau avec un graphe G = (V,E) (où V est l’ensemble des som­mets repré­sen­tant les nœuds et E l’ensemble des arêtes cor­res­pon­dant aux liens, que nous allons sup­po­ser non orien­tés). Nous avons uti­li­sé la loi d’Ohm pour réduire le pro­blème à l’observabilité de la ten­sion en chaque som­met. Nous avons affec­té une variable de déci­sion boo­léenne à chaque som­met, qui prend la valeur 1 si nous ins­tal­lons un cap­teur sur ce som­met, et 0 dans le cas contraire.

Propagation de l’observabilité

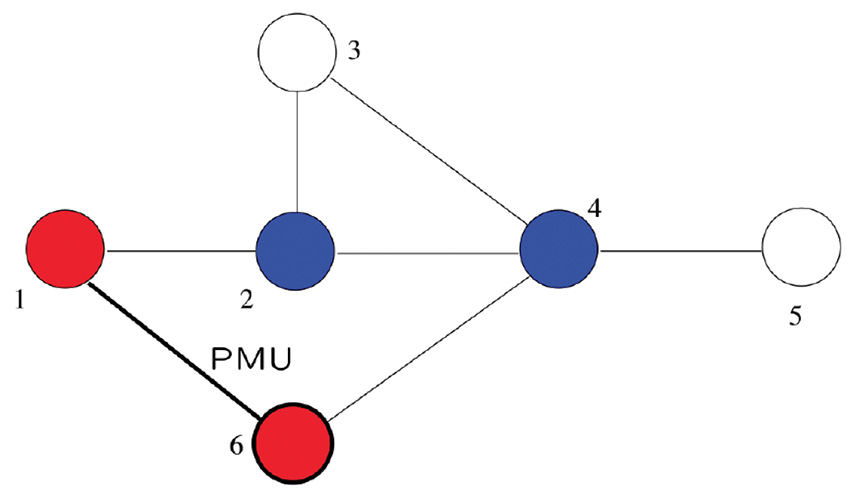
La loi de Kir­ch­hoff, une loi fon­da­men­tale de l’électricité, peut éga­le­ment être prise en compte. Cette loi dit que la somme des cou­rants entrant et sor­tant des arêtes adja­centes à un som­met don­né est zéro. La consé­quence sur l’observabilité des ten­sions aux som­mets, par la loi d’Ohm, est sur­pre­nante : si nous connais­sons la ten­sion à un som­met don­né ain­si que celle de tous ses som­mets adja­cents sauf un, alors nous pou­vons faci­le­ment cal­cu­ler la ten­sion en ce der­nier som­met sans devoir la mesu­rer direc­te­ment. Après cette opé­ra­tion, nous pou­vons encore véri­fier si d’autres situa­tions simi­laires ont été créées grâce aux nou­velles ten­sions cal­cu­lées. Si de telles situa­tions existent, nous cal­cu­lons les ten­sions aux som­mets cor­res­pon­dants. Nous consta­tons donc que cette opé­ra­tion se répète jusqu’à l’épuisement des oppor­tu­ni­tés. Pour illus­trer ce pro­ces­sus de pro­pa­ga­tion de l’observabilité don­né par un posi­tion­ne­ment de cap­teurs, consi­dé­rons l’exemple sui­vant (voir shé­ma page 52). Le cap­teur, dont le nom tech­nique est Pha­sor Mea­su­re­ment Unit (PMU), est ins­tal­lé sur le som­met 6 en direc­tion du câble repré­sen­té par l’arête {1, 6}. Ce PMU mesure la ten­sion au som­met 6 et le cou­rant sur l’arête {1, 6}. Par la loi d’Ohm nous dédui­sons la ten­sion au som­met 1. Main­te­nant nous sommes dans la situa­tion évo­quée pré­cé­dem­ment : nous connais­sons la ten­sion au som­met 1, et toutes les ten­sions aux som­mets adja­cents sauf une, i.e. celle du som­met 6 mais pas du som­met 2. En uti­li­sant la loi de Kir­ch­hoff et ensuite celle d’Ohm, nous pou­vons cal­cu­ler éga­le­ment la ten­sion au som­met 2. Il en est de même pour l’arête {4, 6} et le som­met 4. L’observabilité se « pro­page » ain­si à tra­vers le graphe : nous connais­sons la ten­sion aux som­mets 1, 2 et 4, nous pou­vons donc la cal­cu­ler au som­met 3. Le lec­teur pour­ra faci­le­ment véri­fier que nous pou­vons obser­ver toutes les ten­sions et tous les cou­rants du réseau à par­tir de l’installation d’un seul PMU sur le som­met 6 le long du câble {1, 6}.

“Nous disposons d’outils logiciels très avancés,
qui permettent la résolution de problèmes de taille considérable
en temps limité”

Dynamique de l’observabilité

Il est donc clair que l’observabilité est un pro­ces­sus dyna­mique : à chaque étape, nous véri­fions s’il existe un som­met dont sa ten­sion et celles de ses som­mets adja­cents sont connues, à l’exception d’une seule. Nous cal­cu­lons alors cette ten­sion. Cette nou­velle obser­va­tion peut engen­drer d’autres pos­si­bi­li­tés simi­laires. Le pro­ces­sus s’achève lorsqu’il n’y a plus de pareilles situa­tions. À ce point, nous contrô­lons si la ten­sion est connue à tous les som­mets. Si tel n’est pas le cas, un PMU sup­plé­men­taire doit être ins­tal­lé pour obser­ver d’autres ten­sions à de nou­veaux som­mets, et le pro­ces­sus est réité­ré. Pour for­mu­ler un pro­gramme mathé­ma­tique qui décrive cor­rec­te­ment ce pro­ces­sus, il fau­drait ajou­ter des variables de déci­sion : à la place d’avoir une variable boo­léenne par som­met, nous aurons besoin d’une variable par som­met et par pas de temps (qui sert à décrire le pro­ces­sus dyna­mique). Nous obte­nons alors une for­mu­la­tion valide, mais avec beau­coup de variables pour pou­voir la résoudre dans des délais accep­tables. Une solu­tion à cette dif­fi­cul­té s’obtient en consi­dé­rant qu’une fois obser­vé, tout som­met reste obser­vé : nous disons alors que la dyna­mique de l’observabilité est mono­tone. Une théo­rie due à Tars­ki nous assure alors qu’il y a un plus petit point fixe unique de cette dyna­mique. Nous avons démon­tré que ce point fixe cor­res­pond à l’ensemble des som­mets obser­vés lorsque le pro­ces­sus dyna­mique arrive à ter­mi­nai­son. En géné­ral, un point fixe y d’une fonc­tion φ satis­fait l’équation :

φ (y) = y, (2)

dite de point fixe. Modé­li­ser le point ter­mi­nal de la dyna­mique de l’observabilité avec un point fixe nous per­met de ne plus indexer les variables de déci­sion par pas de temps : il nous suf­fit de défi­nir une variable boo­léenne par som­met. Nous déri­vons donc une nou­velle for­mu­la­tion basée sur l’Éq. (2). Cepen­dant cette for­mu­la­tion est non-linéaire, car elle intègre deux mini­mi­sa­tions imbri­quées : celle pour la réduc­tion du nombre des PMU ins­tal­lés, et celle pour l’obtention du plus petit point fixe. Une fois encore, cette nou­velle for­mu­la­tion est trop dif­fi­cile à résoudre. Heu­reu­se­ment, nous pou­vons obte­nir une for­mu­la­tion où toutes les fonc­tions sont linéaires, avec un seul opé­ra­teur de mini­mi­sa­tion, et un nombre limi­té de variables. Ces types de pro­blèmes res­tent NP-dif­fi­ciles, mais en pra­tique nous dis­po­sons d’outils logi­ciels très avan­cés, qui per­mettent la réso­lu­tion de pro­blèmes de taille consi­dé­rable en temps limité.

Références

[1] Bien­stock (D.), Elec­tri­cal Trans­mis­sion Sys­tem Cas­cades and Vul­ne­ra­bi­li­ty : an Ope­ra­tions Research View­point, Num­ber 22 in MOS-SIAM Opti­mi­za­tion, SIAM, Phi­la­del­phia, 2016.

[2] King (R.), « Infor­ma­tion ser­vices for smart grids », in Power and Ener­gy Socie­ty Gene­ral Mee­ting, volume 2008, Pis­ca­ta­way, 1–5. IEEE.

[3] Poi­rion (P.-L.), Tou­ba­line (S.), D’Ambrosio (C.), and Liber­ti (L.), « The power edge set pro­blem », Net­works, 68(2):104–120, 2016.

[4] Poi­rion (P.-L.), Tou­ba­line (S.), D’Ambrosio (C.), and Liber­ti (L.), « Algo­rithms and appli­ca­tions for a class of bile­vel MILPs », Dis­crete Applied Mathe­ma­tics, April 2018.

[5] Zava­la (V.), Constan­ti­nes­cu (E.) and Ani­tes­cu (M.), « Eco­no­mic impacts of advan­ced wea­ther fore­cas­ting on ener­gy sys­tem ope­ra­tions », in Power and Ener­gy Socie­ty : Confe­rence on Inno­va­tive Smart Grid Tech­no­lo­gy, pages 1–8, Pis­ca­ta­way, 2010, IEEE.

---

Articles similaires :

Un défi colos­sal pour la recherche, la for­ma­tion et l’innovation Le sto­ckage de l’énergie élé­ment clé de la tran­si­tion énergétique De nou­veaux géné­ra­teurs à la fron­tière entre phy­sique et mécanique Le bâti­ment intel­li­gent, nou­veau venu dans la tran­si­tion énergétique Tran­si­tion éner­gé­tique : l’enjeu managérial