Salaires et applications mathématiques
Le salaire est l’un des éléments importants pour la motivation du personnel et donc pour le succès de l’entreprise. Force est de constater qu’il y a peu d’articles sur ce sujet dans La Jaune et la Rouge.
Est-ce à dire que les méthodes de notation du personnel sont tellement parfaites, ou tellement sclérosées, qu’il est inutile de chercher à faire mieux ?
Dès que je suis entré dans l’industrie privée, j’ai été décontenancé par la procédure. Le taux moyen d’augmentation, fixé surtout par des considérations budgétaires, était communiqué aux chefs de service. Huit jours plus tard, j’avais des listes de propositions d’augmentations individuelles et éventuellement des modifications de classement. Je n’avais plus qu’à signer en ajoutant mes propres demandes pour une dizaine de cas. Ces listes contenaient nombre d’informations importantes pour l’avenir des intéressés et celui de l’entreprise, sans que personne ne se pose de questions sur la manière dont les listes avaient été établies.
Les droites de Henry
| Un très bon notateur |
| Un notateur pessimiste |
|
| Un notateur élitiste |
|
| Un mauvais notateur |
|
Les droites de Henry, que j’aimais bien utiliser, sont venues à mon secours pour juger les critères et la qualité de jugement d’un responsable. Pour ceux qui ont tout oublié, je rappelle qu’une transformation permet de changer une courbe intégrale de Gauss en une droite, ce qui change des problèmes de probabilités en de simples exercices de géométrie. Une distribution gaussienne est caractérisée par une droite révélant une population homogène. Dans le cas des augmentations de salaires, on trouve le plus souvent deux ou trois segments de droites, caractéristiques de populations hétérogènes.
Chaque point sur le graphique » gausso-arithmétique » correspond à un salarié déterminé, classé en abscisse dans l’ordre croissant des augmentations. L’ordonnée représente le pourcentage d’augmentation du salarié, la moyenne imposée servant d’unité (il y a possibilité de variantes).
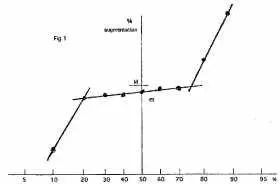
1. Un très bon notateur
Ce bon notateur fait apparaître (à gauche) des » trop payés, à freiner » (moins de 10 % du total, les nouveaux embauchés étant exclus). Il récompense aussi un certain nombre de » très bons » (jusqu’à 20 %, à droite). La médiane (m) est de l’ordre de 90 à 95 % de la moyenne M.
Ce notateur tisse le succès et l’avenir de l’entreprise. Il mérite lui-même une forte augmentation à condition qu’il ait de la suite dans les idées et propose des solutions pour les très mauvais (changement de métier, voire d’entreprise…) et pour les très bons (formation complémentaire, orientation de carrière…).
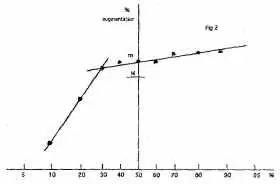
2. Un notateur pessimiste
Il n’y a que deux populations, les » trop payés » (hors nouveaux embauchés) et les » moyens » qui bénéficient ainsi d’un report d’augmentations.
Ce notateur est bien pessimiste sur la nature humaine puisqu’il ne voit aucune qualité à exploiter parmi son personnel. Son principal défaut est de ne pas repérer les personnes à promouvoir dans l’entreprise.
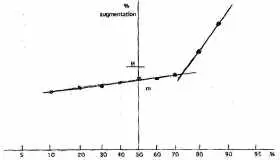
3. Un notateur élitiste
Voici un notateur très élitiste. Il n’y a pas d’individu franchement mauvais. Un petit nombre de très bons sont récompensés et le reste plonge dans une certaine médiocrité. Ce notateur a tendance à défendre ses troupes, mais répugne à se séparer d’un élément douteux. Les performances de l’entreprise finiront par être plombées par ce manque de décision.
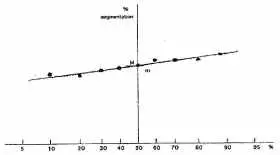
4. Un mauvais notateur
Le graphique est réduit à une droite de faible pente (se reporter au paragraphe n° 1, dans le cas, jamais vu, où la pente est forte).
Ce notateur cumule tous les défauts cités précédemment. Il est bon de se poser des questions sur ses capacités d’encadrement, et peut-être sur son avenir dans l’entreprise.
Le nombre de personnes à noter
Pour repérer les segments de droites, il faut disposer d’un certain nombre de points. En pratique, 8 points sont un minimum mais il est inutile de disposer de plus de 16 points, car cela n’améliore plus la précision des segments de droites.
La géométrie rejoint ici la psychologie. Dans une grande entreprise, un notateur, qui a moins de huit personnes à charge, conduit à une forte hétérogénéité entre notateurs. Son avis est nécessaire, mais doit être pondéré par » l’étage au-dessus « . Au-delà de quinze, le notateur n’est plus assez proche de son personnel pour juger correctement toutes les personnes.
Les droites de Henry apportent des informations utiles sur la façon de noter de chaque chef et limitent le travail d’analyse sur chaque cas. Par contre, elles restent une vue instantanée de la situation, sans lien avec le passé et sans homogénéité d’un notateur à un autre. Il me fallait trouver autre chose.
Les graphes orientés
Chacune des augmentations des secrétaires avait été raisonnable, et pourtant elles étaient les premières à récriminer. Ce fut la première anomalie à attirer mon attention : le groupe des secrétaires n’était pas harmonieux (je parle des salaires).
Je suis parti des discours tenus par les chefs de service pour justifier une demande d’augmentation : » M. A est meilleur que M. B, il est plus autonome, plus ancien, plus âgé, plus diplômé, il présente mieux devant un client, etc. » Pour me souvenir des diverses appréciations, j’ai commencé un graphe orienté (avec des abréviations) représentant les » liaisons entre les salaires » telles qu’elles étaient souhaitées par les chefs de service.
Le graphe hiérarchique
| Exemple d’arc sur un graphe |

|
| N1 = nom du notateur n° 1, 30 = B doit gagner 30 euros par mois de plus que A. Raisons invoquées : T = technicité, Di = Diplômes, Rc = relations avec les clients, Au = Autonomie, Ag = Âge, An = Ancienneté, etc. |
| Le graphe hiérarchique |
|
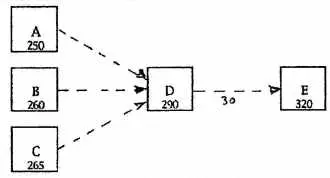
Au début, tout juste sorti du milieu militaire, je suis tombé dans le piège du graphe » hiérarchique » : en chaque point du graphe arrivent plusieurs arcs, mais il ne part qu’un seul arc vers le salaire supérieur.
Ce graphe ne porte que sur cinq personnes A, B, …, E, mais il faut l’imaginer étendu à toutes les personnes sur lesquelles porte l’étude. Les chiffres sous les noms sont les salaires mensuels (ou annuels…). Les chiffres éventuels sous les flèches sont les différences de salaires. Les notateurs sont les chefs hiérarchiques et ne sont donc pas cités.
Le graphe » hiérarchique » était une impasse, mais il permettait déjà quelques remarques intéressantes :
- il permettait de concentrer sur une page format A3 les informations relatives à près de 70 personnes ;
- très souvent, le chef de service se coupait et estimait A meilleur que B, puis six mois plus tard, estimait B meilleur que A. Cette tactique permet de faire attendre B en lui promettant une augmentation » la prochaine fois » ;
- quel est le passé des personnes peu augmentées ? Ont-elles été embauchées récemment (il est habituel de voir leurs salaires freinés pendant un certain temps) ? Notées par le même notateur ? Faut-il envisager un changement de service, de métier ou d’entreprise ?
- pour les embauchés plus anciens, quelles ont été les augmentations dans les années précédentes ? Le notateur était-il différent ?
- la comparaison des augmentations d’une année sur l’autre révèle-t-elle un réel progrès ou un travail exceptionnel méritant seulement une prime ?
L’information contenue dans un graphe hiérarchique est pauvre et se résume à » Chacun gagne moins que son chef « .
Les relations transversales invariantes
| Exemple simple de relations transversales (non hiérarchiques) : différents chefs peuvent avoir des critères de jugement différents. Il n’est donc pas rare d’aboutir à des situations telles que : Salaire de A < Salaire de B < Salaire de C < Salaire de A Ces relations montrent que A, B et C doivent avoir des salaires voisins sinon égaux. C’était le cas d’une partie des secrétaires. |
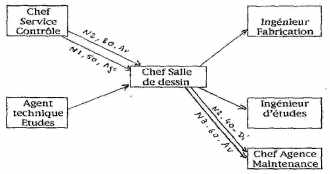
| Exemple complexe de relations transversales ayant duré plus de cinq ans |
|
| Les relations hiérarchiques ne sont pas indiquées. |
Pour justifier une augmentation, un chef de service se réfère très souvent à des personnes en dehors de son propre service : » Mon » ingénieur ne peut pas gagner moins que M. Untel (d’un autre service) : il est plus diplômé (ou plus ancien, etc.). Après être sorti du milieu militaire, j’ai mis un certain temps à comprendre que la partie essentielle du discours du chef de service était précisément celle qui spécifiait des relations entre personnes de différents services.
J’obtenais ainsi sur le graphe hiérarchique des relations transversales, liant des personnes qui n’ont pas un chef immédiat en commun. Ces relations sont invariantes dans le temps (du moins sur plusieurs années). Elles sont confidentielles par nature, parce qu’elles mettent en cause deux personnes, mais les arguments sont repris en partie (hormis les noms) dans les entretiens annuels prévus par la loi.
Les relations transversales ajoutent des contraintes à celles provenant du graphe hiérarchique. Elles m’obligeaient, par exemple, à donner au chef de la salle de dessin une augmentation proche de la moyenne. Si je lui avais attribué moins, j’aurais eu des problèmes pour maintenir un écart raisonnable avec le contrôle de fabrication, une partie de la fabrication, une partie des techniciens d’études et de maintenance, etc. Si je lui avais accordé davantage, j’aurais eu des difficultés à maintenir la moyenne M, notamment pour des ingénieurs et cadres de la fabrication, des études et de la maintenance.
Les » plannings PERT » permettent de fixer pour chaque tâche une » date au plus tôt » et une » date au plus tard « . Il existe de même un salaire calculé via les salaires inférieurs et un autre calculé via les salaires supérieurs. La différence donne la marge de manœuvre pour fixer le salaire. Dans l’exemple cité, la marge était négative d’où nécessité d’arbitrage entre les souhaits des chefs de service.
Les relations transversales atténuent l’hétérogénéité entre les notateurs et, selon mon expérience, » fixent » directement environ 10 % des salaires dans l’entreprise. Les relations hiérarchiques font le reste.
Les résultats
Droites de Henry et graphes sont des méthodes empiriques complémentaires. Elles ont été développées dans quatre entreprises dans le domaine de l’électromécanique, de l’électronique et de l’informatique sur une durée de dix-huit ans et sur des effectifs de 40 à plus de 600 personnes. Pour quels résultats ? Impossible d’affirmer une relation directe avec les salaires, mais dans une période de forte agitation, il n’y a eu aucune grève, sauf une grève de solidarité en faveur d’un Espagnol et, bien sûr, Mai 68 (mais était-ce une grève ? L’établissement était en grande banlieue et il n’y avait pas de transports).
Ce document n’est qu’une exégèse des pratiques habituelles dans les entreprises aux procédures pas trop rigidifiées. Il montre que l’on ne compare pas seulement un individu à lui-même ou à des individus possédant le même » grade » dans la hiérarchie. La progression individuelle se fait en réalité par rapport au » centre de gravité » d’un groupe informel, personnalisé et confidentiel, mais parfaitement identifié par les discours des notateurs.
Pourquoi n’ai-je pas publié ce document plus tôt ? Dans le climat post-soixante-huitard, ce n’était pas le moment d’attiser inutilement les passions en officialisant des méthodes qui sont pourtant, à mon sens, la meilleure façon de tenir compte de tous les avis et donc de tenter de donner à chaque salarié le sentiment qu’il est » à sa place « .