Observations complémentaires sur l’analyse statistique des observations du pendule paraconique de Christian Marchal

I. L’Analyse de Marchal

1. La correspondance des deux fréquencigrammes de Marchal et d’Allais

I. L’Analyse de Marchal

1. La correspondance des deux fréquencigrammes de Marchal et d’Allais

La cor­res­pon­dance pour la série de Bou­gi­val des deux fré­quen­ci­grammes (Figures I A et I B, pages 70 et 71 de l’ar­ticle de Mar­chal) est effec­ti­ve­ment très frap­pante. Elle le serait encore bien plus si le Gra­phique I B de Mar­chal por­tait en ordon­nées les car­rés de l’am­pli­tude r des com­po­santes pério­diques comme mon Gra­phique I A repré­sen­ta­tif des éner­gies rela­tives (L’A­ni­so­tro­pie, Gra­phique XXVI, page 156).

Par exemple sur le Gra­phique I A quatre périodes appa­raissent par­ti­cu­liè­re­ment signi­fi­ca­tives. Elles se retrouvent sur le Gra­phique I B.

Les périodes sont pra­ti­que­ment iden­tiques. Pour les ampli­tudes on a de même et par exemple :

Gra­phique I A :
0,0522÷0,0364 = 1,434.
Gra­phique I B :
(12,89/10,53)2 = (1,224)2 = 1,498.

Les petites dif­fé­rences consta­tées s’ex­pliquent par le fait que le Gra­phique I A a été cal­cu­lé à par­tir de 721 valeurs horaires alors que le Gra­phique I B a été cal­cu­lé à par­tir de 2 160 valeurs de 20 mn en 20 mn (2160÷3 = 720).

2. Corrélation entre les séries 4 et 7 de Saint-Germain et Bougival

• Mar­chal écrit (page 70) :
« Cepen­dant nous ne trou­vions aucune cor­ré­la­tion signi­fi­ca­tive entre les séries simul­ta­nées 4 et 7 de Saint-Ger­main et Bougival. »

• Il n’y a à cela rien d’é­ton­nant. En fait j’ai indi­qué (L’A­ni­so­tro­pie de l’Es­pace, page 147, note 6) :

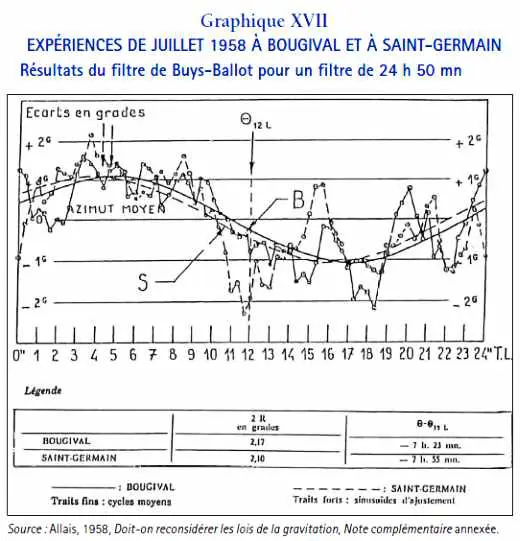
« Les concor­dances moyennes de l’a­na­lyse des séries de Bou­gi­val et de Saint-Ger­main par le filtre de Buys-Bal­lot pour une période de 24 h 50 mn sont d’au­tant plus remar­quables que les courbes jour­na­lières à Bou­gi­val et à Saint-Ger­main dif­fé­raient assez sensiblement. »

Je pré­sente ci-joint la com­pa­rai­son des résul­tats cor­res­pon­dant à la période de 24 h 50 mn à Bou­gi­val et à Saint-Ger­main (L’A­ni­so­tro­pie de l’Es­pace, Gra­phique XVII, page 146).

• En outre comme je l’ai indi­qué (Ani­so­tro­pie de l’Es­pace, page 147) :

« On constate qu’au cours du mois de juillet 1958, les effets de la période de 24 h 50 mn sont sen­si­ble­ment les mêmes dans les deux labo­ra­toires. Les effets des périodes de 24 h et 12 h sont par contre de signe opposé. »

C’est là « une cir­cons­tance tota­le­ment inex­pli­quée à ce jour » (L’A­ni­so­tro­pie de l’Es­pace, page 147, note 5).

Au regard des ampli­tudes rela­tives des périodes de 24 h 50 mn, 24 h, et 12 h, et de leurs signes oppo­sés (L’A­ni­so­tro­pie de l’Es­pace, Tableau IX, page 149), il n’y a rien d’é­ton­nant à ce que la cor­ré­la­tion entre les deux séries d’ob­ser­va­tions ne soit pas significative.

• Mar­chal indique que l’a­jus­te­ment sinu­soï­dal des deux séries de Bou­gi­val et de Saint-Ger­main par les moindres car­rés donne :

Bou­gi­val : azi­mut ~ 161,4 + 1,2 gr sin(L – 165°),
Saint-Ger­main : azi­mut ~ 161,2 + 0,9 gr sin(L – 150°).

Les deux moyennes sont peu dif­fé­rentes des valeurs arron­dies indi­quées sur le Tableau I de L’A­ni­so­tro­pie de l’Es­pace, page 92, soit 161 et 164.

Les deux ampli­tudes 2R : 2,4 et 1,8 sont peu dif­fé­rentes de celles cor­res­pon­dant à l’a­na­lyse de Buys-Bal­lot soit 2,17 et 2,10 (L’A­ni­so­tro­pie de l’Es­pace, Gra­phique XVII, page 146).

La dif­fé­rence de phase 165° – 150° = 15° soit 1 heure est peu dif­fé­rente de celle de 32 mn cor­res­pon­dant à l’a­na­lyse de Buys-Bal­lot (L’A­ni­so­tro­pie de l’Es­pace, Gra­phique XVII, page 146).

Les dif­fé­rences peuvent s’ex­pli­quer par le fait que l’a­na­lyse de Buys-Bal­lot (Ani­so­tro­pie, page 96, note 1) dif­fère tota­le­ment dans son prin­cipe de l’a­na­lyse des moindres car­rés (L’A­ni­so­tro­pie de l’Es­pace, page 101, note 12).

• Mar­chal ajoute (page 71) :

« Cepen­dant les pré­cau­tions d’u­sage, que l’on ne pou­vait guère prendre en 1960 étant don­né la lon­gueur des cal­culs, conduisent à modé­rer cet enthousiasme.

« Tout d’a­bord, même si l’on met à part les très rares « grandes excur­sions », l’é­cart-type des résul­tats par rap­port à la droite de régres­sion, soit 3,5 grades envi­ron, est beau­coup plus impor­tant que l’am­pli­tude des réso­nances obser­vées ce qui est évi­dem­ment très défavorable.

« Ensuite, et sur­tout, si l’on ana­lyse sépa­ré­ment les deux quin­zaines d’une expé­rience on ne retrouve plus du tout les mêmes réso­nances ce qui n’est pas très éton­nant étant don­né l’im­por­tance du bruit de fond mais est évi­dem­ment très gênant quant à l’interprétation.

« Enfin les tests plus com­plexes mais mieux adap­tés que l’a­na­lyse de Fou­rier clas­sique à l’é­tude des phé­no­mènes très brui­tés (test du maxi­mum de vrai­sem­blance ou de Kol­mo­go­rov-Smir­nov, etc.) conduisent eux aus­si à des conclu­sions miti­gées : il y a quelque chose mais on ne sait pas quoi et à ce jour l’on ne peut pas être sûr que la Lune ou le Soleil jouent un rôle impor­tant dans les oscil­la­tions du pen­dule paraconique… »

En fait, qu’en est-il ? Quelle est la por­tée réelle de ces observations ?

a. Sur l’é­cart-type de 3,5 grades je n’ai jamais dit que la seule com­po­sante inté­res­sante était la période de 24 h 50 mn.

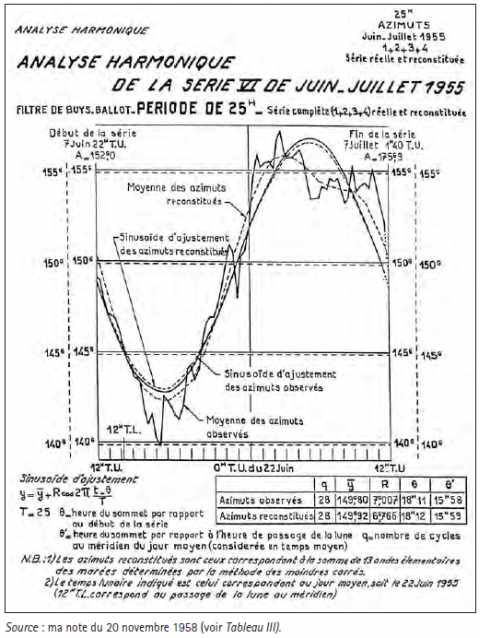
En fait, j’ai pré­sen­té (L’A­ni­so­tro­pie de l’Es­pace, p. 99) les résul­tats de l’a­jus­te­ment de la série de juin-juillet 1955 avec les 13 périodes de la théo­rie des marées. Cet ajus­te­ment a été effec­tué à la fois par le Ser­vice hydro­gra­phique de Paris et l’Ins­ti­tut hydro­gra­phique de Hambourg.

En fai­sant la somme des 13 com­po­santes pério­diques don­nées par cette ana­lyse on obtient une série que j’ai appe­lée « série recons­ti­tuée » (L’A­ni­so­tro­pie de l’Es­pace, pages 105–112).

b. Les ana­lyses par le filtre de Buys-Bal­lot de la série ori­gi­nale et de la série recons­ti­tuée avec un filtre de 25 h (en rem­pla­ce­ment de 24 h 50 mn pour sim­pli­fier les cal­culs L’A­ni­so­tro­pie de l’Es­pace, page 98) sont pra­ti­que­ment iden­tiques comme l’in­dique le gra­phique ci-contre (L’A­ni­so­tro­pie de l’Es­pace, Gra­phique VIII, page 110).

c. En ce qui concerne la décom­po­si­tion par quin­zaine les ana­lyses faites avec le filtre de Buys-Bal­lot sur la série de juin-juillet 1955 montrent que l’on trouve les mêmes résul­tats pour la série ori­gi­nale et la série recons­ti­tuée (L’A­ni­so­tro­pie de l’Es­pace, Gra­phique IX, page 111).

d. Si on com­pare les résul­tats de Bou­gi­val et de Saint-Ger­main pour les quin­zaines, il est évident au regard de ces indi­ca­tions que l’on ne peut retrou­ver les mêmes sinu­soïdes de 24 h 50 mn en rai­son de l’exis­tence des autres com­po­santes pério­diques, dont celles de 24 h et 12 h de signes oppo­sés à la com­po­sante de 24 h 50 mn.

e. En ce qui concerne les tests, le test le plus éla­bo­ré rela­ti­ve­ment à la struc­ture pério­dique d’une série de termes auto­cor­ré­lés est mon test géné­ra­li­sant le Test de Schus­ter (qui ne s’ap­plique qu’à des séries de termes indé­pen­dants, ce qui n’est pas le cas des séries obser­vées). D’ailleurs Mar­chal en sou­ligne la valeur scientifique.

Or, pour Bou­gi­val, l’ap­pli­ca­tion de ce test à l’onde de 24 h 50 mn (L’A­ni­so­tro­pie de l’Es­pace, Gra­phique XXVI, page 156, et Gra­phique I A de Mar­chal) donne une pro­ba­bi­li­té de sur­ve­nance par hasard de P = 0,07 %, ce qui en ana­lyse sta­tis­tique est tota­le­ment signi­fi­ca­tif.

f. Il n’y a pas de « bruit de fond » inex­pli­qué dès lors que l’on consi­dère non pas la seule onde de 24 h 50 mn mais l’en­semble des 13 ondes pério­diques de la théo­rie des marées.

g. Ces consi­dé­ra­tions montrent que les doutes sug­gé­rés par Mar­chal sont tota­le­ment injus­ti­fiés.

En fait, les résul­tats que j’ai pré­sen­tés sur l’a­na­lyse har­mo­nique de mes résul­tats pour les sept séries men­suelles, et tout par­ti­cu­liè­re­ment ceux rela­tifs à Bou­gi­val et Saint-Ger­main, sont par­fai­te­ment éta­blis et ils ne peuvent lais­ser sub­sis­ter aucun doute.

II. L’analyse des sept séries d’observations avec les périodes de la théorie des marées

Dans ma lettre du 22 sep­tembre 1997 à Chris­tian Mar­chal accom­pa­gnant l’en­voi, sur sa demande, des Tableaux des sept séries d’ob­ser­va­tions enchaî­nées du pen­dule para­co­nique à sus­pen­sion ani­so­trope, j’ai par­ti­cu­liè­re­ment insis­té sur l’in­té­rêt tout à fait excep­tion­nel de l’a­na­lyse de mes séries numé­riques avec les périodes de la théo­rie des marées³.

Dans le cas du pen­dule à sus­pen­sion ani­so­trope je n’ai pu à l’é­poque effec­tuer cette ana­lyse que pour la série de juin-juillet 1955 à Saint-Ger­main (Ani­so­tro­pie, Tableau II, page 99)⁴.

En l’es­pèce le tra­vail consi­dé­rable était l’en­re­gis­tre­ment des quelque 15 000 obser­va­tions cor­res­pon­dant aux sept séries du pen­dule para­co­nique à sup­port ani­so­trope. Cet enre­gis­tre­ment étant effec­tué, il suf­fi­sait alors de faire par­ve­nir au Ser­vice hydro­gra­phique et océa­no­gra­phique de la Marine⁵ les sept séries d’ob­ser­va­tions pour les trai­ter avec les pro­grammes d’a­na­lyse des obser­va­tions des marées.

Je ne puis que regret­ter que Mar­chal n’ait pas sui­vi cette sug­ges­tion très pres­sante. Cette ana­lyse aurait été en effet extrê­me­ment ins­truc­tive, notam­ment quant à la varia­tion des coef­fi­cients et des phases au cours du temps.

III. Théorie du pendule

J’ai pré­sen­té dans mon ouvrage L’A­ni­so­tro­pie de l’Es­pace (pages 118–129) toutes les indi­ca­tions utiles pour véri­fier le cal­cul des effets luni­so­laires sur le mou­ve­ment du pen­dule d’a­près la théo­rie clas­sique de la gra­vi­ta­tion (voir tout par­ti­cu­liè­re­ment les Tableaux IV à VII)⁶.

Je conçois que leur ana­lyse peut appa­raître à pre­mière vue comme rela­ti­ve­ment com­plexe, mais pour Mar­chal un tel tra­vail ne peut pré­sen­ter aucune dif­fi­cul­té réelle. Je ne puis que regret­ter qu’il ne l’ait pas fait.

En fait, cette ana­lyse a une impor­tance tout à fait excep­tion­nelle puisque la dif­fé­rence entre les effets cal­cu­lés et les effets obser­vés est de l’ordre de 1 à 20 mil­lions⁷.

IV. Répétition des expériences

Mar­chal sug­gère enfin (page 71) de refaire les expé­riences sur le pen­dule. J’en ai moi-même sou­li­gné l’in­té­rêt excep­tion­nel (L’A­ni­so­tro­pie de l’Es­pace, cha­pitre VIII, pages 645–648).

Dans le cadre limi­té de cet article je ne puis que pré­sen­ter quelques observations :

1. Sur l’a­ni­so­tro­pie du sup­port il est hors de doute que la réa­li­sa­tion d’un sup­port iso­trope pré­sente un très grand inté­rêt et j’ai moi-même réa­li­sé deux séries men­suelles d’ob­ser­va­tions en 1959–1960 en adop­tant une tech­nique d’a­na­lyse fon­dée sur des cal­culs de cor­ré­la­tion (L’A­ni­so­tro­pie de l’Es­pace, Cha­pitre II, pages 227–230)^{8 et 9}.

2. Il ne faut pas exa­gé­rer l’in­fluence des billes comme le démontre la série de trois expé­riences enchaî­nées que j’ai pré­sen­tée dans mon ouvrage (L’A­ni­so­tro­pie de l’Es­pace, page 104, Gra­phique VI).

3. Quant à l’in­té­rêt de la réa­li­sa­tion des expé­riences dans le vide, il est très réduit, sinon nul, car l’ob­ser­va­tion conti­nue du mou­ve­ment du pen­dule peut entraî­ner des effets per­vers. L’a­na­lyse théo­rique montre en effet que dans ce cas le plan d’os­cil­la­tion du pen­dule oscil­le­rait lui-même autour de la direc­tion d’a­ni­so­tro­pie de l’es­pace en plu­sieurs heures, ce qui mani­fes­te­ment com­pro­met­trait la déter­mi­na­tion de l’a­zi­mut de ce plan limite¹⁰.

Avec des séries d’ob­ser­va­tions enchaî­nées l’a­mor­tis­se­ment des oscil­la­tions a une impor­tance rela­ti­ve­ment mineure.

4. La réa­li­sa­tion d’ex­pé­riences simul­ta­nées avec des pen­dules iden­tiques dans des loca­li­tés dif­fé­rentes a un inté­rêt excep­tion­nel comme l’ont démon­tré les expé­riences cru­ciales de Bou­gi­val et Saint-Ger­main en juillet 1958 (voir le Gra­phique XVII ci-des­sus, page 32).

V. Conclusion

Au terme de cette ana­lyse très som­maire je ne puis que remer­cier Mar­chal et son équipe de leur tra­vail. De toute évi­dence il s’a­git en l’es­pèce d’une ques­tion com­plexe. Le cal­cul du Gra­phique I B de Mar­chal rap­pro­ché de mon cal­cul du Gra­phique I A pré­sente en tout cas un inté­rêt tout à fait excep­tion­nel en démon­trant la cor­rec­tion fon­da­men­tale de mes calculs.

En outre, l’a­na­lyse de Mar­chal me per­met de pré­ci­ser quelques points tout à fait essentiels.

_________________________________
1. Pour abré­ger je ferai réfé­rence dans ce qui suit à mon ouvrage L’A­ni­so­tro­pie de l’Es­pace, Édi­tions Clé­ment Juglar, mars 1997, Paris.
2. Allais, 1961, Géné­ra­li­sa­tion du Test de Schus­ter, Annexe III B, page 29.
3. J’a­vais par­ti­cu­liè­re­ment insis­té dans cette lettre sur l’ou­vrage fon­da­men­tal de Paul Schu­re­man, 1941, Manual of Har­mo­nic Ana­ly­sis and Pre­dic­tion of Tides, U. S. Depart­ment of Com­merce, Washing­ton (L’A­ni­so­tro­pie de l’Es­pace, page 707). Voir éga­le­ment dans l’in­dex de mon ouvrage (page 728) mes réfé­rences à Schureman.
4. Voir les Tableaux cor­res­pon­dants dans le cas du pen­dule à sus­pen­sion iso­trope (L’A­ni­so­tro­pie de l’Es­pace, page 273, Tableau IV).
5. Je relève dans l’Annuaire 1996, page S. 25, treize noms de poly­tech­ni­ciens des pro­mos 59 à 87, appar­te­nant au Service hydro­gra­phique et océa­no­gra­phique de la Marine.
6. Je rap­pelle que les cor­rec­tions de la théo­rie de la rela­ti­vi­té sont à la sur­face de la Terre de l’ordre de 10^-9 (L’A­ni­so­tro­pie de l’Es­pace, pages 566–567, note 7).
7. L’A­ni­so­tro­pie de l’Es­pace, page 124, et Tableau VII, page 129.
8. Voir notam­ment les Gra­phiques II et III, pages 261–262.
9. Ces expé­riences n’ont pu être pour­sui­vies en rai­son de l’obs­truc­tion de cer­tains membres de l’A­ca­dé­mie des sciences de l’é­poque (L’A­ni­so­tro­pie de l’Es­pace, pages 213–235).
10. Sur ce point tout à fait essen­tiel, voir L’A­ni­so­tro­pie de l’Es­pace (Cha­pitre I, pages 209–210, note 3, et Cha­pitre II, pages 323–325, tout par­ti­cu­liè­re­ment la note 2, page 324).
Il résulte de là que dans le cas du pen­dule à sus­pen­sion ani­so­trope la tech­nique des expé­riences enchaî­nées de 14 minutes toutes les 20 minutes a été par­ti­cu­liè­re­ment appro­priée (id., page 324, fin de la note 2).

---

Articles similaires :

Quelques sou­ve­nirs d’un petit colon fran­çais au Ton­kin (Viêt­nam)… La pro­duc­tion infor­ma­tique, élé­ment majeur du fonc­tion­ne­ment des entreprises Tho­mas Jef­fer­son et l’École poly­tech­nique : à la recherche des chaî­nons manquants Épi­dé­mio­lo­gie environnementale Alfred Gros­ser : réflexion sur le lien franco-allemand