Mathématiques et modélisation en optimisation industrielle
1. Introduction
Le but de cet article est de montrer, en nous appuyant sur différents exemples tirés de projets industriels concrets, quel peut être l’impact de résultats mathématiques, même très abstraits et théoriques, dans le contexte de la modélisation et de la résolution effective de problèmes d’optimisation industrielle.
L’expérience montre que dans une proportion de cas très importante (au moins 50 %), les problèmes qui se posent en optimisation industrielle sont combinatoires en ce sens qu’ils consistent à déterminer une solution (une combinaison) optimale parmi un ensemble de solutions (de combinaisons) fini, mais de cardinalité tellement élevée qu’il n’est pas possible de procéder par énumération complète de toutes les combinaisons.
Les modèles mathématiques pertinents pour modéliser ce type de problèmes ne relèvent pas exclusivement de disciplines mathématiques » traditionnelles » telles que l’analyse, l’analyse fonctionnelle ou la topologie, mais aussi de ce qu’il est convenu d’appeler les mathématiques discrètes.
Nous mettrons l’accent, dans la suite de cet article, sur quelques-uns des principaux outils mathématiques intervenant, de façon essentielle, dans la modélisation et la résolution efficace de problèmes combinatoires tels qu’on peut en rencontrer en optimisation industrielle, en particulier : la programmation linéaire (cf. paragraphe 4) ; la combinatoire polyédrique qui fournit les outils théoriques permettant de construire des algorithmes de résolution exacte pratiquement efficaces pour beaucoup de problèmes combinatoires difficiles (cf. paragraphe 5).
Plusieurs exemples, tirés de projets industriels divers, seront présentés et permettront d’illustrer la façon dont ces outils théoriques peuvent intervenir, d’abord au niveau de la modélisation (en vue du choix de la meilleure représentation possible du problème), puis au niveau de la conception d’algorithmes de résolution efficaces.
S’il est vrai que l’on dispose, depuis quelques années, de logiciels commerciaux généraux performants pour modéliser et résoudre beaucoup de problèmes d’optimisation industrielle (par exemple le logiciel CPLEX de la société Ilog, le logiciel XPress de la société Dash), la capacité de ces outils à résoudre effectivement les problèmes les plus difficiles (du fait de leur taille ou de leur structure) dépend beaucoup de la façon dont les problèmes sont décrits (formulés) préalablement à leur traitement en machine.
Une bonne connaissance et une bonne maîtrise des outils mathématiques présentés ici apparaissent alors indispensables en vue d’une utilisation rationnelle et efficace des logiciels commerciaux, quels qu’ils soient.
2. Un problème d’optimisation combinatoire en productique
Ce type de problème apparaît chaque fois que l’on doit effectuer une sélection de k objets parmi n objets donnés, tout en respectant un ensemble de contraintes binaires d’incompatibilité.
Il peut être décrit de la façon suivante. Étant données n tâches à réaliser et une liste L de couples (i, j), représentant des incompatibilités entre paires de tâches, on veut savoir s’il est possible d’exécuter simultanément k tâches (k entier > 0 donné) tout en vérifiant l’ensemble des contraintes d’incompatibilité : pour tout (i, j) dans L, les tâches i et j ne peuvent être exécutées simultanément.
Dans le langage de la théorie des graphes, ce problème est connu sous le nom de problème de » l’ensemble stable « .
Le graphe de la figure 2 correspond à un exemple où on a n = 6 tâches représentées par les sommets numérotés de 1 à 6, et où les arêtes modélisent des relations d’incompatibilité entre paires de tâches : l’arête (1, 2) exprime le fait que les tâches 1 et 2 ne peuvent être exécutées simultanément.
De même, l’arête (1, 4) exprime l’incompatibilité entre les tâches 1 et 4, etc. Un sous-ensemble de sommets satisfaisant les contraintes d’incompatibilité est encore appelé un ensemble stable du graphe.
On le voit sur cet exemple, il existe une solution pour k = 3 (on peut exécuter trois tâches simultanément, par exemple les tâches 2, 4 et 6), par contre si k = 4, il n’y a pas de solution.
| Figure 2 |
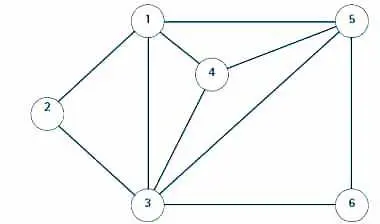 |
| Le graphe des contraintes d’incompatibilité pour l’exemple du problème de sélection de tâches. L’ensemble (2, 4, 6) est une solution de cardinalité maximale k = 3. |
Il est facile de voir que le nombre de solutions d’un tel problème est fini, et majoré par 2n (le nombre de sous-ensembles de tâches).
Le problème de la détermination du sous-ensemble de tâches compatibles de cardinalité donnée paraît donc, a priori, bien simple à résoudre : ne suffit-il pas d’examiner une à une toutes les combinaisons (tous les sous-ensembles de tâches) jusqu’à en trouver une satisfaisant les contraintes du problème posé ?
Néanmoins, la question se complique quelque peu si l’on se préoccupe de la possibilité effective (physique) de résoudre le problème pour des valeurs assez grandes de n (n = 100 ou n = 200 pour fixer les idées). Voyons les chiffres. Pour n = 50, le nombre de combinaisons à tester est supérieur à 106 milliards ; pour n = 100 il est supérieur à 1030 et pour n = 200 il est supérieur à 10 élevé à la puissance 60, un nombre beaucoup plus grand (au dire des spécialistes) que le nombre d’atomes dans l’univers !
En raison du nombre extrêmement élevé de combinaisons à envisager pour le résoudre, le problème d’affectation présenté ci-dessus est qualifié de » combinatoire « .
3. Complexité des problèmes combinatoires : les limites de la technologie
Si on suppose que des ordinateurs sont capables, individuellement, d’énumérer et de vérifier mille milliards de combinaisons par seconde (1012), ce qui est déjà très au-delà des possibilités actuelles de la technologie, et que l’on puisse en faire travailler un million en parallèle, il faudrait alors plusieurs années pour résoudre un problème de taille n = 90 (90 tâches) ; plusieurs millions d’années pour résoudre un problème de taille n = 110 ; et un million de fois plus de temps encore pour un problème de taille n = 130… !
Cette augmentation exponentiellement rapide du nombre de combinaisons a priori, en fonction de la taille du problème (définie ici par le paramètre n), est le phénomène bien connu des praticiens sous le nom » d’explosion combinatoire « . Il montre que si, pour un problème donné (par exemple le problème d’affectation), on ne dispose que de l’approche par énumération, alors, même des progrès considérables dans la technologie des calculateurs ne peuvent reculer que de très peu les tailles limites des problèmes pouvant être effectivement résolus.
Dans l’exemple ci-dessus, un accroissement de performances des ordinateurs dans un rapport de un million ne reculerait la taille limite que de n = 90 à n = 110 environ. Le problème de sélection des tâches présenté dans le paragraphe 2 fait partie d’une classe de problèmes difficiles pour lesquels on ne connaît pas d’algorithme de résolution exacte efficace au sens de la théorie de la complexité (cf. référence [2]).
Parmi les exemples les plus connus de cette classe de problèmes (dits » NP-difficiles »), on peut citer : le fameux problème de Hamilton (souvent appelé problème du » voyageur de commerce ») qui a de très nombreuses applications dans les transports, en logistique, etc. ; le problème dit du » Sac à dos » (cf. encadré 2) qui apparaît dans de très nombreux modèles d’optimisation et dont nous reparlerons plus loin.
Pour la résolution effective de nombreux problèmes difficiles de ce type, les progrès importants qui ont été accomplis depuis une vingtaine d’années apparaissent essentiellement comme le résultat d’analyses mathématiques et algorithmiques approfondies, le progrès des calculateurs électroniques n’y intervenant que fort peu.
Les paragraphes qui suivent vont donner un aperçu des techniques ayant permis ces progrès.
4. Modèles de programmation linéaire : difficulté des problèmes en nombres entiers
La programmation linéaire est un des principaux outils dont on dispose actuellement pour résoudre de grands problèmes d’optimisation.
Un problème de programmation linéaire consiste en la recherche du minimum (ou du maximum) d’une fonction objectif linéaire de n variables réelles x1…, xn, le minimum étant pris sur un sous-ensemble X de Rn (polyèdre) défini par un système linéaire d’égalités ou d’inégalités (cf. encadré 1). Dans ce type de problème, les variables sont autorisées à prendre des valeurs réelles quelconques dans X, on parle de programmes linéaires continus.
De nombreux problèmes industriels peuvent se formuler et se résoudre comme des programmes linéaires continus.
Aujourd’hui, il existe des logiciels commerciaux extrêmement performants tels que CPLEX ou XPress, qui permettent de résoudre de tels problèmes jusqu’à des tailles très importantes.
Des programmes linéaires à quelques milliers de variables et de contraintes sont résolus typiquement en quelques minutes sur un ordinateur type PC ordinaire. Et même la résolution de programmes linéaires à plusieurs centaines de milliers de variables et plusieurs dizaines de milliers de contraintes est devenue parfaitement possible en des temps de calcul raisonnables (typiquement de l’ordre de une à quelques heures).
Cependant cette efficacité remarquable cesse d’être au rendez-vous dès que les problèmes à résoudre comportent – ce qui est malheureusement très fréquent – des restrictions des valeurs possibles des variables à des domaines de valeurs entières. On obtient alors ce que l’on appelle des programmes linéaires en nombres entiers. C’est le cas, dans l’exemple du problème ℗ de l’encadré 1, si on impose, en plus, à la solution cherchée d’avoir ses composantes x1 et x2 entières.
La plupart des problèmes combinatoires difficiles évoqués dans le paragraphe 3 peuvent être aisément formulés comme des programmes linéaires en nombres entiers, ceci explique pourquoi il est a priori beaucoup plus difficile de résoudre un programme linéaire en nombres entiers qu’un programme linéaire continu.
Peut-on néanmoins songer à exploiter la puissance des outils de programmation linéaire continue pour aider la résolution de programmes linéaires en nombres entiers ? L’ensemble des recherches, très actives, menées depuis une bonne vingtaine d’années dans cette direction, a donné naissance à une branche nouvelle des mathématiques appliquées, la combinatoire polyédrique, et a permis d’apporter une réponse positive à cette question.
5. Une théorie de l’approximation des polyèdres
L’idée de départ de la combinatoire polyédrique consiste à essayer de ramener la résolution d’un problème linéaire en nombres entiers à celle d’un simple programme linéaire continu, celui obtenu en substituant à l’ensemble des contraintes décrivant initialement le problème, l’ensemble des contraintes définissant le plus petit polyèdre X contenant toutes les solutions entières (en hachures sur la figure 1 de l’encadré 1).
Malheureusement, on peut montrer que même pour des problèmes en nombres entiers de taille relativement réduite (à partir de quelques dizaines de variables) l’obtention de la liste complète des inégalités permettant de décrire le plus petit polyèdre contenant les solutions entières est impossible en pratique (à cause du nombre extraordinairement élevé d’inégalités nécessaires).
Pour contourner cette difficulté, on doit donc se contenter de travailler avec une description incomplète du polyèdre X, c’est-à-dire avec une approximation construite en n’utilisant que des sous-ensembles particuliers d’inégalités. Encore cela nécessite-t-il une étude approfondie de la structure des polyèdres considérés, afin de caractériser les familles d’inégalités les plus intéressantes (celles conduisant aux meilleures approximations possibles).
En particulier, on s’efforce, chaque fois que possible, de faire en sorte que ces inégalités soient des facettes du polyèdre . Il s’agit là de problèmes ardus, dont la résolution a demandé le développement d’outils théoriques sophistiqués.
Ce type d’approche a jusqu’ici été utilisé avec succès sur des problèmes combinatoires types réputés difficiles comme le problème du » voyageur de commerce « . De nombreuses classes de facettes du polyèdre associé ont pu être mises en évidence, permettant d’obtenir des approximations très précises de ce polyèdre.
Grâce à de tels résultats, il devient alors possible (avec des techniques d’énumération partielle, de type recherche arborescente par exemple) d’obtenir des solutions optimales exactes (et d’apporter la preuve de leur optimalité) en n’explorant seulement qu’une infime fraction de l’ensemble des combinaisons a priori possibles.
On mesurera bien les progrès théoriques et algorithmiques accomplis en observant pour le problème » voyageur de commerce » l’évolution, dans le temps, des records mondiaux des plus grands problèmes résolus, de façon exacte (avec preuve d’optimalité exacte).
Au début des années soixante-dix, à la suite des travaux de Held et Karp on parvenait à résoudre de façon exacte des problèmes jusqu’à une taille de l’ordre de n = 100 (n = nombre de villes = nombre de sommets du graphe).
En 1980, Crowder et Padberg, utilisant la programmation linéaire et la combinatoire polyédrique, trouvent pour la première fois la solution exacte d’un problème de taille n = 318.
En 1987, Padberg et Rinaldi, perfectionnant les mêmes techniques, atteignent la taille n = 532. Les derniers records se situent maintenant au-dessus de n = 10 000 (!).
On peut donc considérer que la discipline a atteint aujourd’hui une maturité certaine, qui lui permet d’envisager la résolution de problèmes d’optimisation industrielle correspondant à des modèles plus complexes, car plus proches de la réalité.
Nous décrivons ci-dessous quelques exemples représentatifs de cette évolution récente vers le traitement d’applications industrielles » en vraie grandeur « .
6. Un problème d’optimisation en transports aériens
Pour réaliser son programme de vols sur une période de temps donnée (une semaine, deux semaines, un mois), une compagnie aérienne doit déterminer une affectation des personnels navigants techniques (PNT) disponibles (pilotes, copilotes) aux différents vols de façon à minimiser le coût total de l’affectation, tout en respectant un certain nombre de contraintes.
| Tableau 1 | Nombre de vols | Nombre de variables | Formulation 1 | Formulation 2 | Facteur de gain T1/T2 | ||
| Nombre de contraintes | Temps T1 (secondes) | Nombre de contraintes | Temps T2 (secondes) | ||||
| P1 | 92 | 2 270 | 9 808 | 83 | 2 098 | 49 | 1,7 |
| P2 | 182 | 6 736 | 42 924 | 1 531 | 6 492 | 573 | 2,6 |
| P3 | 195 | 8 190 | 53 040 | 2 420 | 7 590 | 2 082 | 1,16 |
| P4 | 166 | 6 858 | 47 902 | 1 510 | 6 520 | 541 | 2,8 |
| P5 | 88 | 3 200 | 20 698 | 1 009 | 3 178 | 134 | 7,5 |
| P7 | 94 | 4 360 | 43 114 | 6 852 | 3 914 | 223 | 30 |
| P8 | 59 | 2 520 | 26 546 | (*) | 2 336 | 3 676 | (*) |
| P9 | 68 | 3 060 | 23 436 | 4 880 | 2 636 | 3 676 | 1,3 |
| P10 | 86 | 3 248 | 31 700 | 749 | 2 948 | 32 | 23 |
| P12 | 99 | 7 050 | 76 161 | (*) | 5 421 | 23 195 | (*) |
| P13 | 104 | 7 936 | 87 401 | 6 153 | 6 281 | 3 285 | 1,8 |
| P17 | 104 | 7 968 | 105 290 | (*) | 5 834 | 20 355 | (*) |
| Les résultats affichés (*) correspondent à des problèmes qui n’ont pu être résolus par la formulation 1 de façon exacte au bout de 8 heures de temps calcul. La meilleure solution obtenue au bout de 8 heures est encore à 6,5 % de l’optimum pour P8, à 14,6 % de l’optimum pour P12 et à 6% de l’optimum pour P17. Les mêmes problèmes sont tous résolus de façon exacte en moins de 8 heures avec la formulation 2. | |||||||
La fonction de coût inclut typiquement le total des heures supplémentaires dues (au-delà du temps de vol statutaire, hebdomadaire ou mensuel, un PNT perçoit des heures supplémentaires) et le coût total des » mises en place » (une » mise en place » est nécessaire chaque fois qu’un PNT doit assurer un vol dont l’aéroport de départ ou d’arrivée ne coïncide pas avec sa base de rattachement habituelle).
Divers types de contraintes sont à prendre en compte, en particulier :
– type 1 : des contraintes » d’affectation » : à chaque vol doivent être affectés exactement un pilote et un copilote ;
– type 2 : des contraintes de temps de vol maximum : pour une période de temps donnée (une semaine, un mois), un PNT ne doit pas effectuer un nombre d’heures de vol supérieur à une limite fixée, supposée donnée ;
– type 3 : des contraintes » d’incompatibilité » : un même PNT ne peut être affecté à deux vols devant avoir lieu simultanément (on tient aussi compte, dans l’expression de ces contraintes, de la nécessité, pour un même PNT, de disposer d’un temps minimum entre deux vols successifs auxquels il est affecté).
Si on prend comme variables de décision dans ce problème des variables binaires xij = 0 ou 1 (xij = 1, si et seulement si le PNT i est affecté au vol j, xij = 0 sinon), il est possible de formuler le problème avec un ensemble de contraintes combinant des contraintes d’affectation, des contraintes de » sac à dos » multiples (cf. encadré 2) et des contraintes de type » ensemble stable » d’un graphe (cf. paragraphe 2 ci-dessus).
La première partie du tableau 1 résume les résultats de résolution exacte obtenus avec cette formulation 1 sur une série de douze problèmes réels mettant en jeu jusqu’à 8 000 variables et plus de 100 000 contraintes. Ils concernent la compagnie Tunisair (cf. [9]). Comme le montre le tableau 1, la formulation 1 permet la résolution exacte de 9 problèmes sur 12 dans un temps de calcul inférieur à huit heures avec le logiciel commercial CPLEX (version 6.0.2).
On voit cependant que la modélisation proposée permet d’identifier certaines structures mathématiques du problème que l’on peut ensuite chercher à mieux exploiter, par exemple en mettant en œuvre des méthodes de résolution efficaces bien adaptées à ces structures.
| Encadré 1 |
|
Programmes linéaires continus et en nombres entiers La figure 1 représente l’ensemble X des solutions du programme linéaire à deux variables x1 et x2 et 4 contraintes linéaires d’inégalité ℗ ci-dessous : Maximiser x = x1 + x2 sous des conditions (Un tel programme linéaire est dit continu, les variables pouvant prendre des valeurs réelles quelconques compatibles avec les contraintes. Par exemple x1 = 2.35 et x2 = 1.62 constitue une solution possible de ce problème.) |
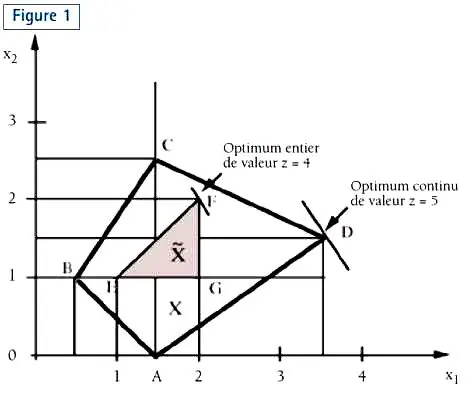 Ensemble X des solutions du programme linéaire ℗. Les points EFG sont les points de X à coordonnées entières. Le plus petit polyèdre contenant ces trois points est indiqué en grisé et noté . |
|
L’ensemble X est constitué du polygone délimité par les 4 points et son intérieur. Il s’agit d’un ensemble convexe appelé polyèdre, dont A B C D sont appelés les points extrêmes (ou encore : les sommets). Il est facile de voir que, parmi tous les points de X, c’est le point D, de coordonnées x1 = 3,5, x2 = 1,5 pour lequel la plus grande valeur de la fonction objectif z est atteinte (z = 5 pour le point D). Les solutions entières du problème ℗ correspondent aux trois points E, F et G et la solution optimale entière correspond à F. On remarque aisément qu’elle peut être obtenue par maximisation de la fonction objectif z sur le polyèdre (en grisé sur la figure) qui est le plus petit polyèdre contenant l’ensemble des solutions entières de ℗. |
Ainsi, une des idées qui a été mise en œuvre avec succès sur ce problème consiste à utiliser des inégalités dites de cliques, classiques pour le problème de stable (cf. paragraphe 2) pour reformuler le problème en remplaçant un grand nombre des contraintes binaires d’exclusion par de telles inégalités. Cette reformulation aboutit, ici, à réduire très sensiblement la taille des problèmes ainsi que l’écart entre la relaxation continue et le problème en nombres entiers à résoudre (on dit que l’on a » renforcé » la formulation), ce qui se traduit par une amélioration très significative de l’efficacité de la résolution (cf. tableau 1, formulation 2). Comme le montre la dernière colonne du tableau 1, les facteurs de gain entre la formulation 1 et la formulation 2 sont souvent supérieurs à 2 et peuvent atteindre 20 ou 30 !
7. Autres problèmes, structures analogues
Il se trouve que les principales structures présentes dans le problème d’affectation d’équipages présenté plus haut (contraintes d’affectation, de stable et de » sac à dos » multiple) apparaissent très souvent dans la modélisation de problèmes d’optimisation industrielle. Nous nous contenterons d’évoquer succinctement ici deux exemples empruntés à des domaines très différents : un problème de planification des tâches (optimisation de plannings de maintenance par exemple) ; un problème d’optimisation de réseaux de télécommunications.
7.1. Un problème de planification de tâches
Il s’agit d’un problème de planification sous contraintes de ressources qui apparaît, par exemple dans le cadre de l’optimisation de plannings de maintenance à EDF [5]. Ce problème admet, bien sûr, de nombreuses variantes qui peuvent se rencontrer dans des domaines d’application très divers (travaux publics, productique, logistique, etc.). Sur une période de temps donnée, découpée en P unités de temps (selon l’application, l’unité de temps peut être l’heure, la minute, la semaine…), on doit réaliser un ensemble de n tâches T1, T2…, Tn en respectant des contraintes diverses, essentiellement des contraintes de précédence et des contraintes de ressources.
Les variables de décision du problème correspondent typiquement au choix pour chaque tâche, d’une date de début. La durée d’exécution de chaque tâche est supposée connue (dans des variantes plus complexes du problème, cette durée peut elle-même dépendre des variables de décision).
Une contrainte de précédence entre deux tâches Ti et Tj exprime le fait que le début de la tâche Tj doit être postérieur au début de la tâche Ti et que l’intervalle de temps entre le début de la tâche Tj et le début de la tâche Ti doit avoir une durée comprise entre deux valeurs extrêmes données.
Les contraintes de ressources concernent un ou plusieurs types de ressources nécessitées par l’exécution des tâches, et peuvent correspondre, par exemple, à des effectifs humains, à des nombres de machines, à des volumes de matières premières, etc. Pour une tâche donnée Ti, la quantité de ressource de type k utilisée au cours d’une période de temps unité pendant l’exécution de la tâche Ti est supposée connue et donnée.
Une contrainte sur la ressource n° k s’exprime alors en imposant qu’à chaque période de temps la somme des quantités de la ressource k, utilisées pour toutes les tâches en cours d’exécution, soit inférieure ou égale à la quantité totale de ressource disponible (supposée connue).
On peut montrer :
- que les contraintes de précédence peuvent s’exprimer par un ensemble de contraintes binaires d’incompatibilité (du même type que celles intervenant dans le problème de l’ensemble stable d’un graphe, cf. paragraphe 2) ;
- que les contraintes de ressources peuvent s’exprimer par un ensemble de contraintes du type de celles intervenant dans le problème de » sac à dos » (cf. encadré 2).
À titre d’exemple, le problème de maintenance posé par EDF [5] pour un exemple de planification sur trois ans, l’unité de temps étant la semaine, avec un nombre de tâches de l’ordre de 150, conduit typiquement à un nombre de variables binaires de l’ordre de 3 000 à 5 000 et à un nombre de contraintes de l’ordre de 15 000 à 20 000.
Compte tenu de la taille de ces problèmes, un travail important de modélisation s’est révélé être nécessaire avant d’aboutir à une efficacité de résolution suffisante. Ainsi, une reformulation des contraintes binaires d’incompatibilité a permis de résoudre effectivement de tels problèmes en des temps de calcul inférieurs à deux heures, et avec une précision meilleure que 1 % sur la valeur de l’optimum.
| Encadré 2 | ||||||
|
Le problème de “ sac a dos ” (simple et multiple) Le problème de “ sac à dos ” (simple) peut se poser de la façon suivante. On considère n objets numérotés i = 1…, n, chaque objet étant défini par deux paramètres, sa valeur vi > 0 et son poids pi > 0. En supposant qu’on est capable de transporter un poids total maximum de valeur P (donnée), le problème est de constituer le chargement transportable de valeur maximale (la valeur d’un sous-ensemble d’objets est évidemment définie comme la somme des valeurs des objets appartenant au sous-ensemble). Un exemple avec n = 6 et P = 12 |
||||||
| Objets | 1 | 2 | 3 | 4 | 5 | 6 |
| Valeurs | 11 | 1 | 20 | 16 | 9 | 7 |
| Poids | 6 | 1 | 9 | 8 | 5 | 4 |
|
Du fait de la petite taille de cet exemple, la solution optimale (qui correspond à la sélection des objets 4 et 6) est aisément obtenue par énumération des 26 = 64 sous-ensembles d’objets. Elle a pour valeur 23. Une formulation simple du problème en programmation linéaire en nombres entiers est possible en associant à chaque objet i une variable entière xi égale à 0 ou à 1, en convenant que xi = 1 si et seulement si l’objet i est sélectionné. On a alors à maximiser z = 11 x1 + x2 + 20 x3 + 16 x4 + 9 x5 + 7 x6 en satisfaisant, en plus de la contrainte : 6 x1 + x2 + 9 x3 + 8 x4 + 5 x5 + 4 x6 ≤ 12, avec les conditions xi ∈ [0, 1] et xi entier pour tout i = 1… 6. Une extension naturelle du problème de “ sac à dos ” simple est le problème de “ sac à dos ” multiple qui fait intervenir plusieurs contraintes de “ sac à dos ” simple. Ce type de structure apparaît dans de nombreux modèles d’optimisation industrielle (cf. paragraphes 6 et 7). |
||||||
7.2. Un problème de réseaux de télécommunications
Le problème évoqué ici apparaît, sous des formes diverses, dans de nombreux contextes, que ce soit au niveau des grands opérateurs de Télécom, ou au niveau des réseaux de communication d’entreprises. Il consiste à déterminer comment construire, au moindre coût, un réseau de télécommunications capable de satisfaire la demande en trafic, supposée connue des usagers ou des clients.
La difficulté du problème tient, d’une part à sa taille (le nombre de flux de trafic à écouler croît comme le carré du nombre de nœuds du réseau), d’autre part à la structure des fonctions de coût (qui sont discontinues).
Un modèle et une méthode de résolution exacte ont été proposés dans [7] qui ont permis, pour la première fois, la résolution exacte d’un ensemble de problèmes-tests particulièrement difficiles. La modélisation utilisée fait intervenir des structures que nous avons déjà rencontrées, puisqu’elle utilise une reformulation du problème combinant des contraintes de type » affectation « , avec des contraintes de type » sac à dos » multiple (cf. encadré 2).
8. Conclusions
Comme les différents exemples mentionnés dans cet article l’ont fait apparaître, la façon dont on modélise un grand problème d’optimisation industrielle de structure complexe est déterminante pour l’efficacité des techniques de résolution qui peuvent lui être appliquées.
Dans les années récentes, diverses approches regroupées sous le vocable de » programmation par contraintes » ont tenté d’aborder ce problème difficile de l’interaction entre formulation et résolution sous l’angle de la programmation logique et de l’intelligence artificielle (cf. [3]). De nombreux logiciels de résolution de problèmes combinatoires ont ainsi été développés, dont certains sont disponibles commercialement (par exemple : Chip de la société Cosytec, Ilog Solver de la société Ilog).
Néanmoins, dans ces systèmes, les algorithmes de résolution proposés (de type » énumération implicite ») ne sont généralement pas en mesure de résoudre de façon exacte des problèmes difficiles de grandes dimensions tels que ceux présentés dans les paragraphes 6 et 7.
Des recherches actuellement en cours visent précisément à améliorer leur efficacité par une intégration des techniques de programmation linéaire et de combinatoire polyédrique évoquées plus haut.