Effet dynamo : de la production industrielle d’électricité au champ magnétique des étoiles
À la fin du xixe siècle, la confrontation des lois de l’électromagnétisme à celle de la mécanique a permis l’élaboration de la théorie de la relativité. Ce qui est moins connu, bien que cette découverte ait permis la production industrielle de la majeure partie de l’électricité que nous consommons, c’est qu’à la même époque Siemens et Wheatstone montraient comment transformer de l’énergie mécanique en énergie électromagnétique en exploitant un mécanisme d’instabilité.
Le même processus se manifeste de manière plus spectaculaire encore à travers l’apparition d’un champ magnétique spontané dans les planètes et les étoiles. Mais, dans ces dynamos naturelles, aucun bobinage ne contraint la géométrie des courants électriques et l’énergie mécanique disponible provient d’écoulements fortement turbulents. Comment expliquer, dans ces conditions, l’existence de champs magnétiques cohérents à grande échelle ? Plusieurs expériences en cours sur des écoulements de sodium liquide devraient nous aider à mieux comprendre les mécanismes complexes à l’œuvre dans ces objets astrophysiques.
De l’induction électromagnétique à la production d’électricité
En 1831, Faraday découvre le phénomène d’induction : une variation de flux de champ magnétique à travers un circuit conducteur produit un courant électrique. Cette variation peut être obtenue par la mise en mouvement de la source du champ par rapport au circuit. La dynamo de bicyclette exploite cet effet élémentaire. On peut noter que, dans cette première application simple, le champ magnétique de l’aimant existe au préalable, indépendamment de la mise en mouvement du galet d’entraînement. Par ailleurs, la bobine où apparaît le courant a une géométrie fixée une fois pour toutes.
En 1867, Siemens met en évidence une conséquence subtile du phénomène d’induction. Dans le cadre d’un dispositif dénué de champ magnétique préalable, plus sophistiqué que la simple dynamo de bicyclette, il montre qu’un courant électrique peut quand même être engendré à partir d’un travail mécanique. Dans ce type de dispositif (figure 1), la géométrie du circuit électrique est choisie de sorte qu’une perturbation initiale de champ magnétique est amplifiée par le courant induit résultant du mouvement du rotor.
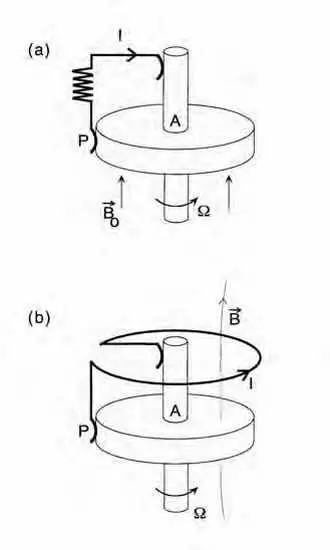
Figure 1 – Induction unipolaire
a) La rotation à vitesse angulaire Ω d’un disque conducteur soumis à un champ magnétique B0 engendre une force électromotrice proportionnelle à Ω et B0 entre A et P. Si l’on ferme le circuit à l’aide de balais, un courant I circule donc dans la résistance.
b) La difficulté rencontrée par Siemens et Wheatstone, qui utilisaient des dispositifs beaucoup plus compliqués que celui de la figure, consistait à engendrer un courant sans appliquer un champ magnétique externe B0.
L’idée est de choisir la géométrie du circuit électrique afin d’utiliser le courant induit pour engendrer le champ magnétique B nécessaire.
On est ainsi conduit à un problème typique d’instabilité : une perturbation de champ engendre un courant qui à son tour amplifie le champ si le sens de rotation est choisi convenablement en fonction de l’induction mutuelle entre le circuit et le disque et si ce dernier tourne suffisamment vite pour compenser les pertes par effet Joule.
On a donc un mécanisme typique d’instabilité conduisant, au-delà d’une vitesse angulaire critique, à la création d’un courant et du champ magnétique associé. Dans les configurations les plus simples, une analyse montre que cette vitesse est donnée par le rapport entre la résistance du circuit et l’induction mutuelle entre le rotor et le stator. La force de Laplace tend à s’opposer au mouvement du rotor et un opérateur extérieur doit donc fournir un travail mécanique afin de maintenir le courant électrique et le champ magnétique créés, qui sont limités par la puissance mécanique disponible. L’effet dynamo consiste ainsi à produire de l’énergie électromagnétique à partir d’un travail mécanique, sans champ magnétique imposé. C’est le principe de base des alternateurs et dynamos industriels.
En 1919, Larmor propose un mécanisme analogue au précédent afin d’expliquer l’origine du champ magnétique du Soleil. Le mouvement d’un conducteur solide y est remplacé par l’écoulement d’un fluide conducteur de l’électricité. À une perturbation de champ magnétique est associé un champ électrique dans le référentiel lié aux particules fluides en mouvement. Il en résulte donc un courant qui, à son tour, engendre un champ magnétique. Si celui-ci renforce la perturbation initiale, on obtient une dynamo qui produit de l’énergie électromagnétique à partir de la puissance mécanique disponible dans l’écoulement.
Cependant, une difficulté se présente immédiatement par rapport au cas des dynamos industrielles. La géométrie des courants induits n’est pas fixée au sein du fluide, celui-ci présentant en général une conductivité électrique homogène dans l’espace. Ainsi, il n’est pas évident a priori que l’effet dynamo soit possible dans un fluide, ou plus généralement, dans tout milieu de conductivité électrique homogène dans l’espace où les courants peuvent circuler librement. Il a même été démontré que l’effet dynamo est impossible si le système physique considéré possède trop de symétries ; c’est le cas par exemple d’un écoulement plan ou encore de toute configuration avec un écoulement et un champ magnétique axisymétriques.
Mécanismes et défis des dynamos fluides turbulentes
Ces » théorèmes anti-dynamo » ont sans doute eu un impact négatif sur le sujet. En effet, mis à part des exemples assez artificiels, il faut attendre les années soixante-dix pour découvrir les premières configurations simples de dynamo homogène. En 1972, Roberts calcule le seuil de l’effet dynamo pour un écoulement sous la forme d’un réseau carré périodique de tourbillons alternés. L’année suivante, Ponomarenko montre qu’un seul tourbillon en contact électrique avec un milieu conducteur infini peut également engendrer un champ magnétique. L’ingrédient essentiel de ces deux écoulements est la présence simultanée de composantes de vitesse axiale et azimutale au niveau de chaque tourbillon, de sorte que l’hélicité moyenne est non nulle. Il en résulte que l’écoulement n’est pas invariant par symétrie miroir.
L’importance de l’hélicité dans les mécanismes de base de la dynamo avait été comprise qualitativement par Parker dès 1954, qui avait constaté qu’elle avait pour effet de déformer les lignes de champ magnétique en engendrant une composante de courant parallèle au champ initial. Cet effet, baptisé » effet alpha « , induit un couplage entre les différentes composantes du champ magnétique, qui n’existe pas en l’absence d’écoulement.
Ce n’est qu’en 2000 qu’ont eu lieu les premières mises en évidence expérimentales d’un effet dynamo engendré par l’écoulement de sodium liquide, à partir de l’écoulement de Roberts à Karlsruhe et de celui de Ponomarenko à Riga. De nombreux problèmes restent cependant à comprendre. En premier lieu, quel est l’effet de la turbulence sur la dynamo ? Celle-ci est de fait difficilement évitable car même dans le sodium, dont la conductivité électrique est la plus élevée parmi les métaux liquides disponibles, le champ magnétique diffuse par effet Joule 100 000 fois plus vite que la quantité de mouvement ne diffuse par viscosité.
La dynamo ne pouvant être engendrée que lorsque l’advection par l’écoulement (l’entraînement par le fluide en mouvement) domine la diffusion Joule, il en résulte que l’importance relative de l’advection par rapport à la diffusion visqueuse, c’est-à-dire le nombre de Reynolds, Re, est gigantesque, supérieur au million dans tous les cas connus. Il est donc clair que les champs magnétiques d’objets astrophysiques (galaxies, étoiles, planètes) sont engendrés par des écoulements moins ordonnés que ceux qui ont pu être étudiés analytiquement ou même numériquement.
Dans les expériences de Karlsruhe et de Riga, les fluctuations turbulentes de grande échelle ont été supprimées par les contraintes géométriques, afin de se rapprocher le plus possible des modèles de dynamo laminaire qui les ont inspirées. Le champ magnétique y est engendré par la partie cohérente de l’écoulement, c’est-à-dire son champ de vitesse moyen au cours du temps.
Or, de nombreux modèles phénoménologiques développés dans le contexte des dynamos astrophysiques semblent indiquer qu’un effet dynamo peut aussi être obtenu lorsque la moyenne du champ de vitesse est nulle, c’est-à-dire uniquement à partir des fluctuations turbulentes. La mise en évidence expérimentale d’une telle dynamo engendrée par un écoulement non contraint et donc turbulente à grande échelle est un enjeu majeur. L’intérêt n’est pas seulement de se rapprocher (un peu) des conditions de fonctionnement des dynamos astrophysiques ou géophysiques ; il est également fondamental de comprendre comment un champ possédant une partie cohérente à grande échelle spatiale peut être engendré par des fluctuations désordonnées.
Quelles sont les caractéristiques d’une instabilité se produisant à partir d’un état désordonné ? Des phénomènes qualitatifs nouveaux par rapport à ceux associés aux bifurcations d’états stationnaires ou périodiques existent-ils ? La réponse à ces questions nécessite, si l’on veut aller au-delà de modèles phénoménologiques de type champ moyen, le développement de nouveaux outils mathématiques.

Boucles de champ magnétique à la surface du Soleil, visualisées lors de la mission spatiale TRACE (Stanford-Lockheed Institute for Space Research, and part of the NASA Small Explorer program).
Une autre question concerne les mécanismes de saturation du champ magnétique engendré par effet dynamo. Autrement dit, peut-on estimer l’énergie magnétique par unité de volume qu’il est possible d’obtenir par effet dynamo à partir des caractéristiques du fluide et de l’écoulement ? Un calcul perturbatif au voisinage du seuil n’est possible que dans le cas d’un écoulement laminaire. Il prédit des champs magnétiques 1 000 fois plus faibles que ceux qui ont été mesurés dans les expériences de Karlsruhe et de Riga. Il a été observé récemment qu’une approche phénoménologique négligeant la viscosité du fluide lorsque l’on estime la réaction de la force de Laplace sur l’écoulement, ce qui semble justifié dans la limite où l’écoulement est fortement turbulent, permet d’obtenir des prédictions en meilleur accord avec les résultats expérimentaux. Cela montre qu’un modèle laminaire ne peut pas permettre l’estimation d’une valeur pertinente pour les champs magnétiques des étoiles ou des planètes. En plus du caractère turbulent de l’écoulement, l’effet de la force de Coriolis doit être pris en compte.
Les champs magnétiques d’objets astrophysiques ont des valeurs qui vont de10-10 tesla pour le champ de notre galaxie, à 102 – 104 tesla pour certaines naines blanches, et même jusqu’à 108 tesla dans le cas d’étoiles à neutrons. La compréhension des différents mécanismes de saturation du champ magnétique permettrait de tirer des informations relatives à la structure interne des écoulements qui l’engendrent. Cela est également vrai dans le cas de la dynamo terrestre, à condition de mieux en comprendre les mécanismes, ce qui est l’objectif d’une expérience réalisée au LGIT (Grenoble).
Le champ magnétique des galaxies pose un autre type de problème, celui du temps de croissance du champ engendré par effet dynamo. Si celui-ci est de l’ordre de l’échelle de temps de diffusion par effet Joule, comme certains modèles le prédisent, on obtient un temps de croissance supérieur à l’âge de la galaxie. Certains écoulements possèdent des propriétés géométriques particulières qui permettent d’amplifier un champ magnétique sur l’échelle de temps associée à l’écoulement et donc indépendante de la conductivité électrique du fluide. Si la dynamo galactique fonctionnait suivant ce mécanisme, cela permettrait l’amplification suffisamment rapide d’un champ magnétique à petite échelle mais n’explique pas l’existence d’une composante de champ magnétique cohérente à l’échelle de toute la galaxie.
Enfin, comme toute instabilité, la dynamo nécessite une perturbation initiale. Dans une expérience de laboratoire, c’est le champ magnétique terrestre ; dans un alternateur industriel, un faible champ magnétique est souvent imposé afin d’amorcer le régime autoentretenu. Mais quel est alors le germe de champ magnétique à partir duquel les champs magnétiques galactiques ont été amplifiés par effet dynamo ? Existe-t-il un mécanisme macroscopique ou faut-il chercher ce champ primordial au niveau des interactions fondamentales ?
Enjeux et perspectives expérimentales
Les problèmes posés par la dynamo turbulente, tant au niveau des instabilités et phénomènes non linéaires que des applications en astrophysique et géophysique, ont motivé depuis quelques années la mise en place de plusieurs expériences sur des écoulements de sodium liquide. Le problème majeur pour réaliser une dynamo turbulente est le choix du type d’écoulement et son dimensionnement, dans la mesure où les nombres de Reynolds mis en jeu rendent impossible toute simulation numérique directe réaliste. Plusieurs expériences à l’étranger et en France tentent actuellement d’observer et d’étudier une dynamo turbulente.
L’expérience » VKS « , réalisée dans le cadre d’une collaboration entre le CEA, l’ENS-Lyon et l’ENS-Paris, a mis en évidence les mécanismes élémentaires de la dynamo turbulente : champ magnétique induit par la rotation différentielle et » effet alpha « . Elle n’a cependant pas permis d’atteindre le seuil d’autoexcitation de la dynamo.
Des expériences similaires, réalisées dans les universités du Maryland et du Wisconsin aux États-Unis, tentent également d’atteindre cet objectif.