De nouvelles techniques pour le contrôle aérien

Le tra­fic aérien a connu une pro­gres­sion très impor­tante pen­dant les der­nières décen­nies et toutes les pré­vi­sions tendent à mon­trer que cette crois­sance ne devrait guère se ralen­tir dans les pro­chaines années. De 1986 à 1996, le tra­fic a connu un accrois­se­ment de 66 % et on pré­voit pour 2006 un accrois­se­ment par rap­port à 1996 de l’ordre de 35 % à 70 % [TM+ 97].
Dans ces condi­tions, la conges­tion du ciel est en passe de deve­nir le fac­teur limi­tant de la crois­sance du tra­fic aérien, du moins en Europe, et la pres­sion des com­pa­gnies aériennes se fait de plus en plus forte pour que la ges­tion du tra­fic soit à la fois plus souple et plus efficace.
Paral­lè­le­ment, les avions s’équipent de moyens sophis­ti­qués (FMS¹, GPS², Data Link) qui devraient per­mettre, à plus ou moins long terme, de chan­ger radi­ca­le­ment les tech­niques de contrôle des aéro­nefs. C’est dans ce cadre qu’est aujourd’hui posé par les com­pa­gnies, sui­vant en cela le RTCA [cotRbod95], le concept du Free Flight (vol sans contrainte), un concept qui ten­drait, sous cer­taines condi­tions, à affran­chir les avions du contrôle aérien tel qu’il est pra­ti­qué aujourd’hui et per­met­trait ain­si aux aéro­nefs de suivre le che­mi­ne­ment de leur choix dans cer­taines zones de l’espace aérien.
Comme nous allons cepen­dant le voir, le che­min à par­cou­rir est encore long avant la mise en place d’un tel concept.

Tour de contrôle Vigie à l’aé­ro­port Charles de Gaulle. © P. GILBERT – AÉROPORTS DE PARIS

Principes généraux

Le but pre­mier du contrôle du tra­fic aérien est d’as­su­rer la sécu­ri­té des aéro­nefs. Le but second, d’as­su­rer un écou­le­ment aus­si opti­mal que pos­sible des flux de tra­fic, en par­ti­cu­lier en termes de retards.

Nous allons tout d’a­bord poser quelques défi­ni­tions indis­pen­sables pour la com­pré­hen­sion du reste de notre exposé.

Route aérienne : le che­mi­ne­ment d’un avion dans l’es­pace est une série de seg­ments de droite, reliant des points de report appe­lés balises. His­to­ri­que­ment, ces balises étaient bien sou­vent des points équi­pés de moyens de radionavigation.

Plan de vol : il contient tous les élé­ments indi­ca­tifs décri­vant le vol pré­vu pour un avion (heure de départ, niveau de vol, route prévue).

Contrôle en route : il s’a­git du contrôle à l’ex­té­rieur des zones entou­rant les aéro­ports (dans ces der­nières, on parle de contrôle d’approche).

Sec­teurs de contrôle : l’es­pace aérien est divi­sé en sec­teurs de contrôle. Chaque sec­teur est confié à un, ou plus sou­vent deux, contrô­leurs, qui ont la charge d’as­su­rer la sépa­ra­tion des aéro­nefs dans cette por­tion de l’es­pace. Le trans­fert d’un avion d’un sec­teur à un autre sec­teur fait l’ob­jet d’une coor­di­na­tion entre les contrô­leurs en charge de cha­cun des deux secteurs.

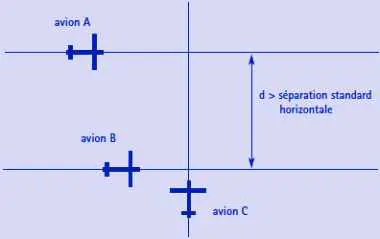
Sépa­ra­tions : on défi­nit une dis­tance hori­zon­tale expri­mée en milles nau­tiques³ (NM), la sépa­ra­tion hori­zon­tale⁴, et une dis­tance ver­ti­cale expri­mée en pieds⁵ (ft), la sépa­ra­tion ver­ti­cale⁶. On dit que deux avions sont sépa­rés quand la dis­tance qui sépare leurs pro­jec­tions sur un plan hori­zon­tal est supé­rieure à la sépa­ra­tion hori­zon­tale ou quand la dif­fé­rence de leurs alti­tudes est supé­rieure à la sépa­ra­tion verticale.

Conflit élé­men­taire : deux avions sont dits en conflit lors­qu’ils ne sont plus sépa­rés. Si l’on se fixe une durée T, deux avions seront dits en conflit poten­tiel pen­dant T, si durant le temps T, ils ont une pro­ba­bi­li­té non nulle⁷ d’être en conflit.

Clus­ter : un clus­ter d’a­vions est une fer­me­ture tran­si­tive d’a­vions en conflits poten­tiels. Si un avion A est en conflit avec B à l’ins­tant t < T (où T est l’ho­ri­zon tem­po­rel explo­ré) et B est en conflit avec C à l’ins­tant t + Dt < T alors A, B et C appar­tiennent au même clus­ter. Ain­si dans la figure 1, les avions A et B ne sont jamais en conflit mais ils appar­tiennent au même clus­ter. Une dévia­tion de C pour évi­ter B peut lui per­mettre d’é­vi­ter A.

L’ex­pres­sion conflit à n avions signi­fie en fait clus­ter à n avions.

Améliorer l’écoulement du trafic

Il existe plu­sieurs approches pour ten­ter d’a­mé­lio­rer l’é­cou­le­ment du tra­fic. Elles se divisent en deux grandes caté­go­ries : d’une part, l’a­mé­lio­ra­tion de l’or­ga­ni­sa­tion de l’es­pace aérien et des flux de tra­fic, d’autre part, l’a­mé­lio­ra­tion du contrôle aérien lui-même.

L’or­ga­ni­sa­tion de l’es­pace et des flux : on peut ten­ter tout d’a­bord d’a­mé­lio­rer la façon dont l’es­pace est décou­pé en sec­teurs. Jus­qu’à pré­sent, ce décou­page a sou­vent été fait de façon empi­rique, et une approche plus scien­ti­fique peut per­mettre d’es­pé­rer une amé­lio­ra­tion capa­ci­tive. Il faut cepen­dant gar­der en mémoire :

1) que le décou­page actuel est le résul­tat d’une longue expé­rience, et qu’il sera dif­fi­cile de l’améliorer,

2) que l’on ne peut aug­men­ter indé­fi­ni­ment le nombre de sec­teurs, car lorsque les sec­teurs deviennent trop petits, la ges­tion des flux entrant et sor­tant devient plus coû­teuse que le contrôle lui-même⁸.

On peut éga­le­ment ten­ter d’a­mé­lio­rer l’é­cou­le­ment des flux en amé­lio­rant les modèles de capa­ci­té sec­teur, en pro­po­sant des tari­fi­ca­tions du contrôle dif­fé­rentes en fonc­tion des horaires, ou en pro­po­sant des routes alter­na­tives aux aéro­nefs pour décon­ges­tion­ner cer­taines zones. Enfin, on peut ima­gi­ner un chan­ge­ment radi­cal du décou­page de l’es­pace en pré­voyant par exemple une zone de type » Free Flight » où le contrôle serait assu­ré dif­fé­rem­ment. Toutes ces tech­niques sont actuel­le­ment à l’étude.

Le contrôle aérien : la prin­ci­pale rai­son des retards obser­vés aujourd’­hui en Europe (et par­ti­cu­liè­re­ment en France) est la satu­ra­tion des sec­teurs de contrôle » en route « . Pour ten­ter d’aug­men­ter la capa­ci­té du contrôle en route, de nom­breuses solu­tions sont à l’é­tude. Les pro­blèmes à trai­ter sont bien iden­ti­fiés : il faut savoir pré­voir les tra­jec­toires des avions, détec­ter les conflits, regrou­per ces conflits par clus­ters, don­ner des manœuvres simples les résol­vant, etc.

Si les pro­blèmes liés à la réso­lu­tion de conflits aériens sont donc bien iden­ti­fiés, les tech­niques à employer le sont moins. Avant de ren­trer dans les détails tech­niques du pro­blème, nous allons nous employer à pré­sen­ter quelques concepts généraux.

Prévision de trajectoires et détection de conflits

Avant de son­ger à résoudre les conflits, il faut d’a­bord les détec­ter. Or, la détec­tion de conflits se base avant tout sur une bonne pré­vi­sion de trajectoires.

Aéro­port Charles de Gaulle, tour de contrôle, salle IFR © P. GILBERT – AÉROPORTS DE PARIS

La pre­mière erreur consis­te­rait à croire que l’on peut consi­dé­rer les vitesses des avions comme constantes. En France, envi­ron trois conflits sur quatre com­prennent au moins un avion qui est en mon­tée ou en des­cente ; or, si l’on prend l’exemple d’un air­bus A320, il va en dix minutes pas­ser d’une alti­tude de 1 000 ft à une alti­tude de 26 000 ft, et sa vitesse va pas­ser de 200 à 400 km/h.

La pré­vi­sion de tra­jec­toires pour­rait donc pas­ser soit par la liai­son de don­nées, auquel cas le FMS de l’a­vion pour­rait ren­voyer une tra­jec­toire rela­ti­ve­ment pré­cise ; cepen­dant, cette pré­vi­sion res­te­rait tout de même tri­bu­taire d’in­cer­ti­tudes externes : si un avion de ligne est capable de suivre pré­ci­sé­ment une route et une alti­tude, maî­tri­ser pré­ci­sé­ment sa vitesse sol n’est pas pos­sible en rai­son notam­ment des vents (une quin­zaine de nœuds).

Il est d’autre part impos­sible de cor­ri­ger en per­ma­nence la vitesse car les réac­teurs ont un régime de consom­ma­tion idéal dont il ne faut pas trop s’é­car­ter. Enfin, ils ne doivent pas, pour des rai­sons méca­niques, être sou­mis à des chan­ge­ments de régime permanents.

Enfin, s’il est impos­sible de récu­pé­rer direc­te­ment les tra­jec­toires cal­cu­lées par les FMS, on peut recou­rir à une simu­la­tion de tra­jec­toires faite à par­tir de modèles pré­éta­blis ; les incer­ti­tudes seront alors extrê­me­ment fortes, en rai­son de nom­breuses incon­nues (masse de l’a­vion, consignes de la com­pa­gnie, etc.).

Ain­si, il est à peu près incon­ce­vable d’es­pé­rer dépas­ser la dizaine de minutes en termes d’ho­ri­zon tem­po­rel pour la pré­vi­sion de trajectoires.

Différentes approches pour l’aide à la résolution

On peut gros­siè­re­ment clas­ser les dif­fé­rentes approches de la façon suivante :

Approche anti-cal­cu­la­toire : la pre­mière approche consiste à construire un modèle, dit » cog­ni­tif « , du contrô­leur, spé­cia­le­ment dans ses modes d’ap­pré­hen­sion des para­mètres du conflit, et d’u­ti­li­ser ce modèle dans un cal­cu­la­teur afin de construire des outils de fil­trage de l’in­for­ma­tion et d’as­sis­tance élec­tro­nique au contrô­leur. Cette méthode a l’im­mense avan­tage d’être faci­le­ment inté­grable au sys­tème de contrôle actuel, car elle s’emploie à chan­ger le moins pos­sible les modes opé­ra­toires existants.

Elle est cepen­dant sous les feux de deux cri­tiques, d’une part, les limi­ta­tions main­te­nant bien connues propres aux approches dites » expertes » ou » cog­ni­tives » : coût très éle­vé de déve­lop­pe­ment et de main­te­nance, pro­blème de géné­ra­li­sa­tion des maquettes au cas géné­ral, dégra­da­tion bru­tale de l’ex­per­tise aux limites du domaine, failli­bi­li­té du sys­tème expert [Dre79, Fox90] ; d’autre part, lais­sant l’homme tota­le­ment en charge de toutes les déci­sions, elle se conten­te­ra de repous­ser le » mur de la capa­ci­té [Vil87] » dont nous par­lions plus haut, sans faire dis­pa­raître les causes fon­da­men­tales de son exis­tence. Il s’a­git donc d’une approche essen­tiel­le­ment à court ou moyen terme.

Auto­ma­ti­sa­tion cen­tra­li­sée com­plète : il existe main­te­nant des débuts de preuves mon­trant que la réa­li­sa­tion d’un sys­tème auto­ma­ti­sé de contrôle n’est pas une pure chi­mère. Dans une telle hypo­thèse, un sys­tème cen­tral gère l’en­semble des avions pré­sents dans l’es­pace, et leur donne les ordres de contrôle néces­saires à la réso­lu­tion des conflits. Cette approche a été abor­dée pour la pre­mière fois par le pro­jet AERA-III [Cel90, SPSS83, NFC+83, Nie89b, Nie89a, PA91] aux États-Unis, ou plus récem­ment le pro­jet ARC 2000 [K+89, FMT93, MG94] du Centre expé­ri­men­tal Eurocontrol.

Le grand avan­tage de cette méthode est qu’elle per­met d’aug­men­ter de façon consi­dé­rable la capa­ci­té de l’es­pace, la flui­di­té de l’é­cou­le­ment du tra­fic et per­met de garan­tir l’op­ti­ma­li­té glo­bale des solu­tions obte­nues. Le prin­ci­pal pro­blème est la tran­si­tion vers un tel sys­tème depuis le sys­tème actuel. Il ne peut donc s’a­gir que d’une approche à long ou très long terme.

Délé­ga­tion de tâches : dans ce cas, l’on tente de réa­li­ser un par­tage dyna­mique des tâches entre l’homme et la machine au sein d’un même sec­teur de contrôle ; l’or­di­na­teur pren­drait en charge cer­tains conflits et lais­se­rait l’homme en charge du tra­fic res­tant. Cette méthode pour­rait être inté­res­sante à moyen terme : elle devrait per­mettre de sou­la­ger l’o­pé­ra­teur en cas de pointe de tra­fic tout en main­te­nant sa vigi­lance et ses qua­li­fi­ca­tions. L’in­con­vé­nient majeur est qu’elle sup­pose une totale confiance de l’homme envers le cal­cu­la­teur, et envers la répar­ti­tion de tra­fic et les réso­lu­tions qu’il exé­cute. Trop peu d’ex­pé­ri­men­ta­tions ont été menées jus­qu’i­ci pour pou­voir conclure.

Approche auto­nome : dans ce type d’ap­proche, on sup­pose que les avions se trou­vant dans une cer­taine zone de l’es­pace (par exemple au-des­sus de 32 000 ft) uti­lisent des sen­seurs et des algo­rithmes embar­qués pour réa­li­ser eux-mêmes la détec­tion et la réso­lu­tion de conflits. Déjà exa­mi­née dans le cadre du pro­jet ATLAS [DA93], le Centre expé­ri­men­tal d’Eu­ro­con­trol tra­vaille dans le cadre du pro­jet FREER à la défi­ni­tion d’al­go­rithmes pou­vant per­mettre la réa­li­sa­tion de ce type de sys­tème ; les docu­ments défi­nis­sant les diverses stra­té­gies de R&D font d’ailleurs une place impor­tante à ce type de méthodes.

Son prin­ci­pal avan­tage est sa rela­tive com­pa­ti­bi­li­té avec le sys­tème actuel : sa mise en place pour­rait se faire pro­gres­si­ve­ment par une tac­tique d’en­cer­cle­ment (en com­men­çant par les espaces trans­océa­niques et les espaces supé­rieurs). D’autre part, elle per­met­trait de don­ner aux avions les tra­jec­toires directes ori­gine-des­ti­na­tion qu’ils demandent à l’in­té­rieur de ces zones » libres « .

Il sub­siste cepen­dant de nom­breux pro­blèmes : d’une part, chaque avion n’a qu’une vision limi­tée du monde qui l’en­toure ; il est donc par­fai­te­ment sus­cep­tible de choi­sir des manœuvres d’é­vi­te­ment à court terme qui peuvent se révé­ler désas­treuses sur le long terme, soit en termes de sécu­ri­té, soit en termes d’ef­fi­ca­ci­té ; il n’existe encore aujourd’­hui aucun algo­rithme ayant prou­vé son effi­ca­ci­té sur des échan­tillons de tra­fic réel. Enfin, les pro­blèmes d’in­ter­face entre les zones » libres » et les zones contrô­lées ont été peu abordés.

Notons enfin que ce type d’ap­proche est par­fois confon­du avec l’A­CAS (Air­borne Col­li­sion Avoi­dance Sys­tem) ; ceci mérite une petite pré­ci­sion. L’ACAS, et par­ti­cu­liè­re­ment son implan­ta­tion actuelle à bord des avions : le TCAS [TCA90], est un sys­tème embar­qué conçu pour faire de l’é­vi­te­ment à très court terme (de l’ordre de la minute). Il s’a­git avant tout d’un sys­tème de der­nier secours pour évi­ter des col­li­sions, et non d’un moyen de contrôle ou de main­tien de séparation.

En fait, le dilemme dans lequel nous nous trou­vons enfer­més est un peu le sui­vant : les outils capa­ci­tifs sont dif­fi­ci­le­ment inté­grables dans le sys­tème actuel, et les outils faci­le­ment inté­grables risquent fort d’être peu capacitifs.

La résolution de conflits

Complexité théorique

Résoudre un conflit impli­quant n avions consiste dans le meilleur des cas à assu­rer les sépa­ra­tions en don­nant aux avions des ordres de manœuvre, tout en mini­mi­sant les allon­ge­ments de tra­jec­toire liés aux dévia­tions induites.

La dif­fi­cul­té du pro­blème est assez facile à appré­hen­der. Pour un conflit à deux avions dans le plan hori­zon­tal, l’es­pace des solu­tions admis­sibles com­prend deux com­po­santes connexes (à condi­tion que les avions ne fassent pas de boucles) : soit l’a­vion 1 passe devant l’a­vion 2, soit il passe der­rière. Un clus­ter à n avions contient n(n‑1)/2 paires d’a­vions. Le nombre théo­rique de com­po­santes connexes est alors de 2 puis­sance n(n‑1)/2. Ceci explique l’é­chec des méthodes d’op­ti­mi­sa­tion locale sur ce type de problème.

Des ten­ta­tives d’é­va­lua­tion de la com­plexi­té théo­rique ont été faites. Il semble pro­bable qu’il s’a­git d’un pro­blème NP-com­plet, une classe de pro­blèmes n’ad­met­tant aujourd’­hui aucun algo­rithme poly­no­mial les résolvant.

Modèle de manœuvre et d’incertitude

Les ordres de manœuvre don­nés aux avions doivent être faci­le­ment com­pré­hen­sibles et exé­cu­tables par les pilotes. On peut, dans le cadre d’une modé­li­sa­tion rela­ti­ve­ment simple, se limi­ter à la typo­lo­gie suivante :

Figure 2 – Modèle de manoeuvre et d’incertitude​

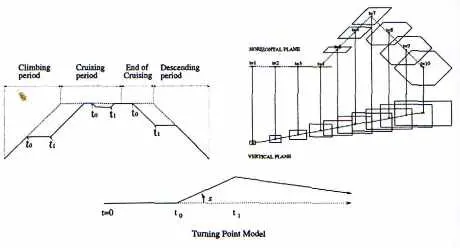• dans le plan hori­zon­tal, un avion peut modi­fier son cap d’un angle s valant 10, 20 ou 30 degrés à l’ins­tant t₀ et reprendre la direc­tion de sa des­ti­na­tion finale à t_t (figure 2) ;
• dans le plan ver­ti­cal, le type de manœuvre dépend de la phase de la tra­jec­toire de l’avion :
  – pen­dant la mon­tée, on peut inter­rompre la tra­jec­toire à t₀ et reprendre la mon­tée à t₁,
  – pen­dant la phase de croi­sière, on peut des­cendre de 1 000 ft à t₀ et reprendre à t₁,
  – la phase de pré­des­cente com­mence une cin­quan­taine de milles nau­tiques avant le début de la des­cente. On peut alors anti­ci­per la des­cente en t₀ et sta­bi­li­ser l’a­vion à t₁,
  – au cours de la des­cente, aucune manœuvre n’est pos­sible dans le plan vertical.

Pour tenir compte des incer­ti­tudes sur les vitesses, on peut modé­li­ser les avions non par des points maté­riels mais par des poly­gones convexes. La taille des poly­gones aug­mente dans la direc­tion de la vitesse. On passe ain­si d’un point t = 0 à un seg­ment, puis un paral­lé­lo­gramme, puis un hexa­gone, etc. Il suf­fit alors de véri­fier, pour que la contrainte hori­zon­tale soit res­pec­tée, que les convexes qui modé­lisent les avions soient sépa­rés par la sépa­ra­tion stan­dard (voir figure 2).

Dans le plan ver­ti­cal, l’in­cer­ti­tude est beau­coup plus forte, on maî­trise très mal le taux de mon­tée d’un avion qui dépend de para­mètres aus­si variés que la masse, ou la mise en route de la cli­ma­ti­sa­tion. En consé­quence, le même prin­cipe que dans le plan hori­zon­tal est repris mais les incer­ti­tudes sont beau­coup plus grandes. On com­prend mieux, en regar­dant la figure 2, l’im­por­tance de la qua­li­té de la pré­vi­sion : les convexes conte­nant l’en­ve­loppe des posi­tions pos­sibles croissent rapi­de­ment, et si les incer­ti­tudes sont trop fortes, le nombre d’a­vions en conflits poten­tiels devient en quelques minutes très, voire trop, impor­tant. D’autre part, une mau­vaise pré­vi­sion peut ame­ner à résoudre des conflits qui n’au­raient en fait pas lieu. Enfin, l’ins­tant de début de manœuvre est com­plè­te­ment dépen­dant de la qua­li­té de la pré­vi­sion et son choix en est ren­du par­ti­cu­liè­re­ment difficile.

Techniques de résolution

On peut trou­ver plu­sieurs approches pour abor­der le pro­blème de réso­lu­tion de conflits.

N. Durand [Dur96] traite le pro­blème comme un pro­blème de com­mande opti­male, F. Médio­ni [MDA94] pro­pose un modèle per­met­tant de le trans­for­mer en pro­blème linéaire, celui-ci demeu­rant for­te­ment com­bi­na­toire. É. Féron [OSF97] pro­pose d’u­ti­li­ser des algo­rithmes de relaxa­tion convexe du pro­blème com­bi­na­toire ini­tial. Toutes ces tech­niques consi­dèrent le pro­blème comme global.

Une autre approche consiste à consi­dé­rer le pro­blème des conflits à n avions comme un pro­blème sépa­rable : des méthodes d’op­ti­mi­sa­tion sont appli­quées suc­ces­si­ve­ment sur cha­cun des avions impli­qués ; il s’a­git alors de résoudre n pro­blèmes rela­ti­ve­ment simples et non un seul pro­blème de grande taille, ceci au détri­ment de la qua­li­té des solutions.

Enfin, une der­nière méthode tend à employer des tech­niques de type réac­tif : dans ce cas, la notion d’op­ti­ma­li­té dis­pa­raît com­plè­te­ment et l’on ne retient que l’ad­mis­si­bi­li­té des trajectoires.

Nous allons rapi­de­ment pré­sen­ter quelques exemples de ces dif­fé­rentes approches.

Un exemple de méthode globale de résolution

Si l’on dis­pose de toutes les infor­ma­tions concer­nant l’en­semble des avions, et que l’on peut agir à sa guise sur un avion plu­tôt que l’autre, le pro­blème de la réso­lu­tion de conflits est un pro­blème d’op­ti­mi­sa­tion glo­bale : pour un conflit à n avions, et sui­vant la modé­li­sa­tion pré­sen­tée ci-des­sus, il s’a­git d’op­ti­mi­ser 3n variables cor­res­pon­dant aux t₀, t₁ et s de chaque avion.

Pour un élé­ment com­po­sé de 3n variables, la fonc­tion d’é­va­lua­tion à opti­mi­ser simule les tra­jec­toires (avec incer­ti­tudes) sur T minutes à venir, mesure les conflits et s’il n’y a pas de conflit, prend en compte le retard dû aux manœuvres, la durée des manœuvres et le nombre total de manœuvres. Une solu­tion sans conflit est tou­jours pré­fé­rée à une solu­tion avec conflit. On mini­mi­se­ra le nombre de manœuvres pour limi­ter le tra­vail des pilotes, la durée des manœuvres pour libé­rer les avions le plus tôt pos­sible pour une éven­tuelle autre manœuvre.

Il existe de nom­breuses méthodes d’op­ti­mi­sa­tion glo­bale sus­cep­tibles d’être appli­quées à ce pro­blème : branch and bound par inter­valles, algo­rithmes A*, recuit simu­lé, etc. Par­mi les dif­fé­rentes méthodes, les algo­rithmes géné­tiques⁹ ont la par­ti­cu­la­ri­té de ne pas requé­rir d’hy­po­thèse sur la fonc­tion à opti­mi­ser (qui peut être le résul­tat d’une simu­la­tion), et de pou­voir four­nir en un temps don­né plu­sieurs solu­tions proches de l’op­ti­mum. Par ailleurs, par­mi les algo­rithmes que nous avons tes­tés seules les méthodes géné­tiques per­mettent de prendre en compte des conflits de grande taille pou­vant aller jus­qu’à une tren­taine d’a­vions [DA96].

Figure 3 – Archi­tec­ture générale

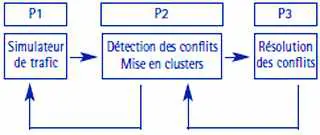L’ar­chi­tec­ture géné­rale de l’al­go­rithme est la sui­vante (figure 3) :

• le pro­ces­sus P1 est un simu­la­teur de tra­fic qui gère l’en­semble des vols pas­sant au-des­sus de la France sur une journée,
• le pro­ces­sus P2 est char­gé de détec­ter les paires d’a­vions en conflit, de fabri­quer les clus­ters d’a­vions par fer­me­ture tran­si­tive des paires d’a­vions en conflit. Il véri­fie éga­le­ment les tra­jec­toires nou­velles pro­po­sées par P3,
• le pro­ces­sus P3 est l’al­go­rithme de réso­lu­tion de conflits pro­pre­ment dit.

Cet algo­rithme a été tes­té sur du tra­fic réel dans le cadre de simu­la­tions [DA97]. Pour une jour­née com­pre­nant 6 388 vols, et en pre­nant une incer­ti­tude de +/- 5 % dans le plan hori­zon­tal et +/- 10 % dans le plan ver­ti­cal, l’al­go­rithme résout tous les conflits (1 694) qui se pré­sentent au-des­sus de 10 000 pieds. Le retard moyen lié aux manœuvres sur l’en­semble des avions est de 5 secondes, et le retard maxi­mal infé­rieur à 4 minutes.

Méthode » diviser pour régner »

Dans ce cadre, pour un pro­blème à n avions, on cherche à résoudre suc­ces­si­ve­ment n pro­blèmes à trois variables, plu­tôt qu’un seul pro­blème à 3n variables.

Figure 4 – Exemple de résolution

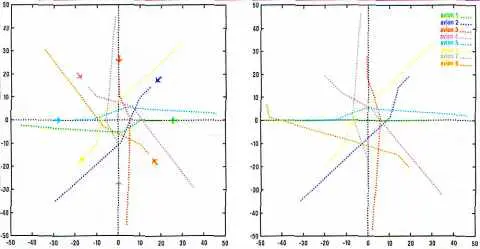Dans un pre­mier temps, on choi­sit une prio­ri­té entre les n avions pour savoir dans quel ordre ils vont construire leur tra­jec­toire, puis cha­cun d’entre eux construit ladite tra­jec­toire en pre­nant comme contraintes les avions déjà pré­sents au moment où il résout. On peut employer là aus­si diverses méthodes pour fabri­quer les tra­jec­toires [AD97, MDA98]. Le pro­blème est rela­ti­ve­ment clas­sique en robo­tique, et des méthodes rela­ti­ve­ment élé­men­taires comme les algo­rithmes A* peuvent en venir aisé­ment à bout dans des temps raisonnables.

On peut voir sur la droite de la figure 4 un tel exemple de réso­lu­tion. Le der­nier avion est lar­ge­ment péna­li­sé par rap­port aux autres. D’autre part, si l’on com­pare cette solu­tion à celle obte­nue par la méthode glo­bale (à gauche de la figure), on constate qu’il est pos­sible de trou­ver une solu­tion de bonne qua­li­té pour tous les avions et qui n’en péna­lise gra­ve­ment aucun.

En fait, cette méthode peut même ne trou­ver aucune solu­tion admis­sible, alors que la méthode glo­bale en trou­ve­ra plu­sieurs. Ain­si, dans le simple cadre d’un conflit à trois avions, l’al­go­rithme échoue­ra si les angles de conver­gence sont faibles et si, de plus, les prio­ri­tés au point de pas­sage sont mal choi­sies. Le pro­blème se trouve ain­si en par­tie repor­té sur le choix de l’ordre de réso­lu­tion, ce qui est loin d’être simple.

Méthodes réactives

Le docu­ment le plus inté­res­sant est cer­tai­ne­ment [Zeg94]. Il intro­duit la notion de coor­di­na­tion d’ac­tions grâce à dif­fé­rentes forces qui s’exercent sur les agents, dans notre cas les avions.

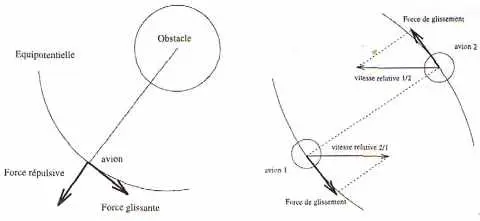
Figure 5 – Force répul­sive et force glis­sante, forces de glis­se­ment coordonnées

La méthode, ini­tia­le­ment déve­lop­pée dans le domaine de la robo­tique ([Kha­tib]), se base sur l’a­na­lo­gie phy­sique d’une charge dans un champ de poten­tiel. Pour l’é­vi­te­ment, le poten­tiel est une mesure du risque de col­li­sion. On défi­nit ain­si trois types de forces qui devront agir sui­vant l’urgence :

• les forces attrac­tives qui per­mettent aux avions d’at­teindre leur objec­tif (une balise ou leur des­ti­na­tion finale par exemple),
• les forces répul­sives qui per­mettent aux avions d’é­vi­ter un obs­tacle proche donc dan­ge­reux. Cet obs­tacle peut être un avion ou une zone interdite,
• les forces de glis­se­ment qui per­mettent de contour­ner les obstacles.

Les avions ont alors une action coor­don­née (voir figure 5). Une force de glis­se­ment est défi­nie de la manière sui­vante : si l’on observe l’é­qui­po­ten­tielle de dan­ger pas­sant par l’a­vion, une force de glis­se­ment est tan­gente à cette équi­po­ten­tielle, alors que la force répul­sive est nor­male. Il y a donc plu­sieurs forces de glis­se­ment pos­sibles. Si l’on reste dans le plan hori­zon­tal, la figure 5 montre que l’on peut défi­nir deux sens de glis­se­ment (droite ou gauche). Le sens opti­mal (il s’a­git ici d’op­ti­ma­li­té locale, pour l’a­vion concer­né) est celui qui favo­rise le rap­pro­che­ment vers l’objectif.

Dans le cas d’un obs­tacle mobile, on défi­nit une action coor­don­née d’évitement.

Pour trai­ter les conflits à plus de deux avions, on addi­tionne les forces rela­tives à chaque avion, confor­mé­ment au modèle phy­sique (addi­tion des poten­tiels). Si les résul­tats pra­tiques sont bons pour de faibles den­si­tés, les expé­riences menées dans le cadre de fortes den­si­tés semblent mon­trer un effon­dre­ment rapide du sys­tème qui en vient à géné­rer plus de conflits qu’il n’en résout. Ceci est lié à la mécon­nais­sance des inten­tions des avions ain­si qu’à la visi­bi­li­té limi­tée de l’en­vi­ron­ne­ment ; dif­fé­rentes amé­lio­ra­tions per­mettent de pal­lier par­tiel­le­ment ces pro­blèmes, sans tou­te­fois par­ve­nir à les résoudre [Bos97].

Conclusion

Au terme de ce rapide sur­vol, il faut avant tout signa­ler que la recherche dans le domaine du tra­fic aérien est une acti­vi­té extrê­me­ment récente. Les tech­niques pré­sen­tées ici ont besoin d’être sou­mises à l’é­preuve du monde opé­ra­tion­nel pour être validées.

Pour­tant, il semble que les bonnes ques­tions com­mencent à être posées ; l’aug­men­ta­tion du tra­fic et les contraintes éco­no­miques ren­dront néces­saires une sérieuse évo­lu­tion des tech­niques de ges­tion du tra­fic aérien. Cer­taines réponses scien­ti­fi­que­ment étayées com­mencent à être appor­tées aux pro­blèmes posés ; il faut cepen­dant se rap­pe­ler que la valeur tech­nique d’une solu­tion ne sera pas le seul cri­tère inter­ve­nant dans les choix qui seront faits dans les années à venir : d’autres fac­teurs comme l’ac­cep­ta­bi­li­té ou la faci­li­té de tran­si­tion seront cer­tai­ne­ment plus déterminants.

_________________________________
1. Flight Mana­ge­ment System.
2. Glo­bal Posi­tio­ning System.
3. 1 mille nau­tique vaut 1 852 m (1 minute d’arc sur un méridien).
4. Elle est de 8 NM en France mais devrait bien­tôt des­cendre à 5 NM.
5. 1 pied vaut 30,48 cm.
6. Elle vaut 1 000 ft au-des­sous du FL 290 et 2 000 au-dessus.
7. Il ne peut y avoir de cer­ti­tude lorsque l’on traite de la pré­vi­sion de tra­jec­toires, les avions étant sou­mis à de nom­breux fac­teurs non com­plè­te­ment connus, comme le vent, par exemple.
8. On estime géné­ra­le­ment que la charge de tra­vail est pro­por­tion­nelle au nombre d’a­vions dans le sec­teur, aux flux entrant et sor­tant, et au nombre de conflits qui se pro­duisent dans le sec­teur. Le modèle théo­rique montre que le nombre de conflits devrait varier avec le car­ré du nombre d’a­vions. Les simu­la­tions montrent en fait qu’il croît, beau­coup plus rapi­de­ment, en rai­son de l’or­ga­ni­sa­tion du tra­fic réel, ce qui ne manque pas d’inquiéter.
9. Les algo­rithmes géné­tiques sont des algo­rithmes d’op­ti­mi­sa­tion s’ap­puyant sur des tech­niques déri­vées de la géné­tique et de l’é­vo­lu­tion natu­relle : croi­se­ments, muta­tions, sélec­tion, etc. Ils ont déjà une his­toire rela­ti­ve­ment ancienne puisque les pre­miers tra­vaux de John Hol­land sur les sys­tèmes adap­ta­tifs remontent à 1962 [Hol62].

---

Articles similaires :

Le contrôle en route de la cir­cu­la­tion aérienne L’aéroport blo­que­ra-t-il le déve­lop­pe­ment du trans­port aérien ? L’évolution des sys­tèmes de sur­veillance et de contrôle des mou­ve­ments au sol des aéroports De nou­veaux sys­tèmes CNS/ATM un enjeu de taille “Fly by wire” ou le pilo­tage électronique