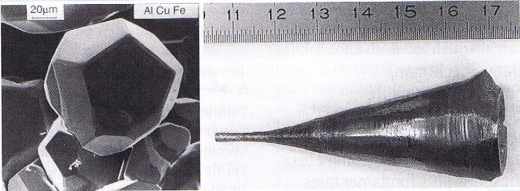
Les quasi-cristaux : quinze ans après, quelques énigmes subsistent…

Au prin­temps 1982, Dany Shecht­man, cher­cheur israé­lien de l’Ins­ti­tut de tech­no­lo­gie Tekh­nion (Haï­fa) en séjour au NBS (aujourd’­hui NIST) à Washing­ton DC, découvre dans un alliage AlMn rapi­de­ment soli­di­fié une phase ayant toutes les carac­té­ris­tiques d’un cris­tal mais pos­sé­dant une symé­trie ico­sa­édrique incom­pa­tible avec la pério­di­ci­té cris­tal­line. Au cours des deux ans qui suivent, Shecht­man cher­che­ra en vain à expli­quer dans le cadre des para­digmes de l’é­poque ses obser­va­tions expé­ri­men­tales d’ap­pa­rence para­doxale. Il devra se résoudre à la conclu­sion que ce solide est un édi­fice ato­mique néces­sai­re­ment non pério­dique mais dont les atomes sont remar­qua­ble­ment ordon­nés à longue dis­tance et ce n’est que fin 1984, qu’il annon­ce­ra, avec trois de ses col­lègues, sa décou­verte dans un article à Phy­si­cal Review Let­ters¹.

La réac­tion de la com­mu­nau­té scien­ti­fique est immé­diate : Dov Levine et Paul Stein­hardt² publient dans le même volume une pre­mière des­crip­tion algé­brique de cet ordre géo­mé­trique nou­veau et intro­duisent le mot » qua­si­crys­tal « . Début 1985, Michel Duneau et André Katz³, cher­cheurs au Centre de phy­sique théo­rique de l’É­cole poly­tech­nique, publient l’ar­ticle fon­da­teur de la méthode moderne de des­crip­tion de ces objets : un qua­si-cris­tal peut être engen­dré en effec­tuant une coupe tri­di­men­sion­nelle d’o­rien­ta­tion irra­tion­nelle d’un objet pério­dique d’un espace de plus grande dimension.

Ici, le mot qua­si-cris­tal est enten­du comme une contrac­tion de » cris­tal qua­si pério­dique » en réfé­rence aux tra­vaux des mathé­ma­ti­ciens H. Bohr⁴ et A. Besi­co­vic⁵ sur les fonc­tions presque pério­diques. Avec les tra­vaux conco­mi­tants des Russes P. A. Kalu­gin, Y. E. Kitaev et L. S. Levi­tov⁶, puis de l’A­mé­ri­cain V. Elser⁷, la méthode de coupe irra­tion­nelle d’un espace de dimen­sion supé­rieure à 3 s’im­pose dès 1986 comme le cadre mathé­ma­tique natu­rel de la des­crip­tion ato­mique des quasi-cristaux.

L’i­mage la plus simple d’un arran­ge­ment qua­si pério­dique est celle ima­gi­née en 1979 – et dans un autre contexte – par le grand phy­si­cien théo­ri­cien anglais Roger Pen­rose8 qui inven­ta un pavage non pério­dique du plan par deux types de tuiles obéis­sant à une loi de construc­tion déter­mi­niste, et dont la figure de dif­frac­tion est consti­tuée de pics fins, comme pour les cris­taux, mais se répar­tis­sant sur des figures à symé­trie penta­go­nale. Ce pavage devint rapi­de­ment l’ar­ché­type des qua­si-cris­taux lors­qu’il fut démon­tré par Katz et Duneau qu’il est le résul­tat d’une coupe bidi­men­sion­nelle irra­tion­nelle d’un objet pério­dique de dimen­sion 4.

Il ne man­quait, pen­sait-on à l’é­poque, que des échan­tillons de taille macro­sco­pique et de bonne qua­li­té pour résoudre le pro­blème cris­tal­lo­gra­phique. Là aus­si, les pro­grès furent très rapides.

Figure 2

Exemples d’alliages qua­si cristallins. À gauche : grains de phase ico­sa­édrique dans l’alliage AlCuFe obte­nus après refroi­dis­se­ment lent. (Cli­ché A. QUIVY, CECM-CNRS, Vitry). À droite : mono­grain macro­sco­pique de la phase ico­sa­édrique de l’alliage AlPdMn obte­nu par soli­di­fi­ca­tion et crois­sance contrô­lée d’un germe (méthode de Czro­crals­ky) à par­tir du bain liquide. (Cli­ché Y. CALVAYRAC, CECM-CNRS, Vitry).

L’al­liage méta­stable ini­tial de la décou­verte de Shecht­man fut bien­tôt sui­vi d’une mul­ti­tude de nou­velles phases, la phase déca­go­nale décou­verte par L. Ben­ders­ky⁹ au NIST, puis des phases stables dans les sys­tèmes AlCuFe et AlPdMn par le groupe de A.-P. Tsai¹⁰ à Sendai.

On réper­to­rie aujourd’­hui plus d’une cen­taine d’al­liages métal­liques (en grande majo­ri­té à base alu­mi­nium) for­mant des phases qua­si cris­tal­lines par simple refroi­dis­se­ment lent des bains de fusion des éléments.

Ain­si, dès le début des années 1990, des modèles ato­miques plau­sibles ont pu être pro­po­sés mais tou­te­fois sans jamais atteindre la pré­ci­sion des déter­mi­na­tions cris­tal­lo­gra­phiques usuelles. La dif­fi­cul­té réside dans le fait que la des­crip­tion d’un qua­si-cris­tal requiert un espace de dimen­sion 6 (pour les struc­tures ico­sa­édriques) en sorte que les para­mètres défi­nis­sant la struc­ture ato­mique sont beau­coup plus nom­breux (a prio­ri en nombre infi­ni) que ceux néces­saires à carac­té­ri­ser un cris­tal ordinaire.

Il faut émettre un cer­tain nombre d’hy­po­thèses phy­siques et géo­mé­triques pour pou­voir trai­ter numé­ri­que­ment ce pro­blème qui, même réduit à la vision idéale la plus simple du » qua­si-cris­tal par­fait « , reste d’une redou­table com­plexi­té. La ques­tion est donc encore ouverte de savoir la ou les­quelles de ces hypo­thèses doivent être modi­fiées pour conduire à un meilleur accord avec les don­nées expérimentales.

Figure 3

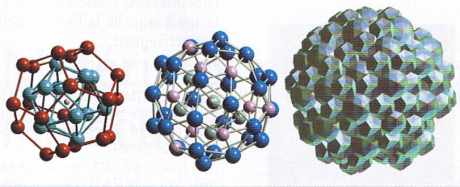Les deux amas ato­miques de gauche (conte­nant res­pec­ti­ve­ment, de gauche à droite, 33 et 50 atomes) consti­tuent les confi­gu­ra­tions ato­miques les plus fré­quentes des struc­tures ico­sa­édriques AlPdMn et AlCuFe. Ces amas s’interconnectent dans l’espace pour don­ner, sur l’image de droite, un ensemble dense ordon­né d’atomes dont la com­pa­ci­té est proche de celle des métaux et alliages CFC usuels.

Quelques points sont cepen­dant soli­de­ment éta­blis. Ain­si, les qua­si-cris­taux réels et les pavages qua­si pério­diques par­tagent des pro­prié­tés essen­tielles. Le pavage, choi­si de façon ad hoc, joue, pour le qua­si-cris­tal, un rôle très ana­logue à celui du réseau de trans­la­tion pour un cris­tal. Tout motif ato­mique de taille finie se répète uni­for­mé­ment dans la struc­ture et toute boule de rayon fini contient un nombre fini de confi­gu­ra­tions ato­miques locales, tou­jours les mêmes quelle que soit la posi­tion de la boule (de même que le pavage de Pen­rose de la figure 1 est engen­dré par deux types de tuiles seulement).

On peut alors don­ner une des­crip­tion sim­pli­fiée des struc­tures ato­miques en décri­vant les quelques types d’a­mas ato­miques les plus fré­quents. Par exemple, près de 95 % des atomes des struc­tures ico­sa­édriques AlCuFe et AlPdMn se répar­tissent sur les deux amas pro­to­types pré­sen­tés sur la figure 3. Ces amas s’in­ter­sectent les uns les autres pour conduire à un assem­blage qua­si pério­dique com­plexe dont la symé­trie moyenne est celle de l’icosaèdre.

Deux ques­tions liées res­tent aujourd’­hui au cœur des pro­blèmes struc­tu­raux, celle de l’o­ri­gine de la sta­bi­li­té ther­mo­dy­na­mique de ces phases et celle de leurs modes de croissance.

Les qua­si-cris­taux exis­tant essen­tiel­le­ment dans les alliages métal­liques, on peut rai­son­na­ble­ment pen­ser que les inter­ac­tions chi­miques domi­nantes entre espèces ato­miques sont celles à courte et moyenne dis­tances. On sait d’autre part que des pavages simples comme celui de Pen­rose obéissent à des règles d’in­ci­dence qui sti­pulent com­ment deux tuiles adja­centes doivent être dis­po­sées pour conduire à un agen­ce­ment qua­si pério­dique à longue dis­tance. Du point de vue phy­sique, ces règles géo­mé­triques indiquent que l’ordre qua­si pério­dique se pro­page par infor­ma­tion locale en bon accord avec l’hy­po­thèse que les inter­ac­tions chi­miques entre atomes sont de por­tée finie.

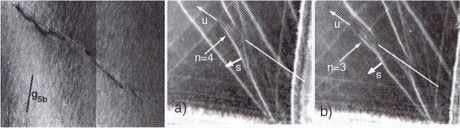
Figure 4

Dis­lo­ca­tions dans les quasi-cristaux. À gauche : obser­va­tion en micro­sco­pie élec­tro­nique à trans­mis­sion de dis­lo­ca­tions dans l’alliage ico­sa­édrique AlPdMn. Au centre et à droite : les tech­niques d’observations modernes dites de fais­ceaux conver­gents aux grands angles (LACBED) qui super­posent des infor­ma­tions du plan focal (espace réci­proque de la dif­frac­tion) et du plan image (espace direct de la struc­ture) per­mettent de carac­té­ri­ser ces défauts direc­te­ment dans le grand espace de dimen­sion 6. (Cli­chés Daniel CAILLARD CEMES/LEO-CNRS, Toulouse).

Une dif­fi­cul­té concep­tuelle majeure appa­raît lors­qu’on prend en compte le fait que ces règles d’in­ci­dence ne sont pas des règles de crois­sance au sens où, lors de la construc­tion du pavage, des situa­tions appa­raissent où l’une ou l’autre des tuiles peuvent être choi­sies qui satis­font éga­le­ment les règles. Le choix requiert alors un exa­men de l’en­semble du pavage déjà construit ; en ce sens la crois­sance n’est pas un pro­ces­sus local et devrait être expo­nen­tiel­le­ment lente pour un qua­si-cris­tal par­fait, ou conduire, la taille aug­men­tant, à des qua­si-cris­taux de plus en plus impar­faits ce qui est en contra­dic­tion avec l’expérience.

Il faut donc ima­gi­ner qu’au voi­si­nage du front de crois­sance il se pro­duit de nom­breux réar­ran­ge­ments ato­miques locaux pour obte­nir une struc­ture idéale émaillée de défauts de posi­tions ato­miques (simi­laires à des lacunes et appe­lés » pha­sons « , terme emprun­té aux struc­tures incom­men­su­rables proches cou­sines des qua­si-cris­taux) dont la dyna­mique, mise en évi­dence par dif­frac­tion qua­si élas­tique de neu­trons par Lyon­nard et Cod­dens¹¹ au LLB-Saclay, est encore mal connue.

Non moins sur­pre­nantes sont les pro­prié­tés élec­tro­niques de ces alliages. Obte­nus à par­tir de métaux bons conduc­teurs (quelques microhms. cm à basse tem­pé­ra­ture), ils pré­sentent des résis­ti­vi­tés excep­tion­nel­le­ment éle­vées (attei­gnant 10⁶ microhms. cm pour les meilleurs qua­si-cris­taux AlPdRe) qui suivent, en tem­pé­ra­ture, une loi de Mat­thie­sen inverse : la résis­ti­vi­té aug­mente lorsque la tem­pé­ra­ture dimi­nue. Il s’a­git là d’un effet de confi­ne­ment des élec­trons dû à la symé­trie qui tend à loca­li­ser les états élec­tro­niques sur cer­tains atomes de ces amas.

Figure 5

À gauche : une image haute réso­lu­tion STM d’une sur­face qui­naire d’un qua­si-cris­tal AlPdMn. Les atomes de sur­face se regroupent en penta­gones eux-mêmes orga­ni­sés selon des penta­gones plus grands. À droite : la super­po­si­tion à une par­tie de l’image mon­trant les posi­tions des atomes d’aluminium telles que pré­vues par un modèle idéal mas­sif du quasi-cristal. (Cli­chés Luc BARBIER SPCSI-CEA, Saclay).

Ce genre d’ef­fet – ren­con­tré dans les sys­tèmes amorphes où il s’ex­plique par une déco­hé­rence rela­tive des élec­trons due au désordre de posi­tion – est ici, au contraire, dû à des effets cohé­rents par­tiel­le­ment des­truc­tifs, impo­sés par l’ordre qua­si pério­dique, et qui donc s’am­pli­fient avec la qua­li­té qua­si cris­tal­line du maté­riau. La conduc­ti­bi­li­té ther­mique des qua­si-cris­taux suit glo­ba­le­ment la même ten­dance – avec par exemple un fac­teur 10 entre la conduc­ti­bi­li­té ther­mique de AlPdMn et celle de l’or – en sorte que, pour des alliages métal­liques, ces maté­riaux sont, à basses tem­pé­ra­tures, d’ex­cep­tion­nels iso­lants thermiques

Les pro­prié­tés méca­niques des qua­si-cris­taux sont simi­laires à celles des phases inter­mé­tal­liques com­plexes à grande maille cris­tal­line. Ce sont des maté­riaux durs et fra­giles. Les dis­lo­ca­tions, défauts linéaires res­pon­sables de la défor­ma­tion plas­tique, sont peu ou pas mobiles, compte tenu des nom­breux réar­ran­ge­ments ato­miques locaux néces­saires à leurs pro­gres­sions. Ces maté­riaux pré­sentent une spec­ta­cu­laire tran­si­tion fra­gile-duc­tile à haute tem­pé­ra­ture, lorsque la mobi­li­té ato­mique devient suf­fi­sante pour per­mettre aux dis­lo­ca­tions de bou­ger en balayant der­rière leur sillage les effets de désordre local du pavage dû à leur pré­sence. On constate alors un phé­no­mène d’a­dou­cis­se­ment de la courbe contrainte-défor­ma­tion qui per­met d’at­teindre une défor­ma­tion de plus de 100 % sans rup­ture et sans que la struc­ture ato­mique qua­si cris­tal­line s’en trouve signi­fi­ca­ti­ve­ment dégra­dée. On passe ain­si bru­ta­le­ment d’un com­por­te­ment fra­gile à un com­por­te­ment duc­tile exa­gé­ré ana­logue à la superplasticité.

Un champ très actif actuel de la recherche sur les qua­si-cris­taux concerne l’é­tude de leurs sur­faces et de leurs modes d’oxy­da­tion. Il est main­te­nant bien éta­bli que, sous réserve d’une pré­pa­ra­tion soi­gnée de net­toyage ionique sous ultra-vide et recuits consé­quents, les sur­faces des qua­si-cris­taux sont elles-mêmes qua­si pério­diques et sont, à des relaxa­tions ato­miques près, des coupes bidi­men­sion­nelles par­ti­cu­lières des struc­tures mas­sives. On dis­pose ain­si de ter­rasses planes où la den­si­té élec­tro­nique varie de façon qua­si pério­dique sur les­quelles on peut envi­sa­ger de gref­fer des molé­cules en des sites pré­fé­ren­tiels reflé­tant cette quasi-périodicité.

La fabri­ca­tion d’un bon qua­si-cris­tal est une opé­ra­tion qui reste aujourd’­hui encore déli­cate en labo­ra­toire. Les com­po­si­tions doivent être ajus­tées avec une grande pré­ci­sion et les trai­te­ments ther­miques, en par­ti­cu­lier à haute tem­pé­ra­ture, par­fai­te­ment contrô­lés, alors qu’on ne connaît avec pré­ci­sion qu’un petit nombre de dia­grammes de phase. Les phases qua­si cris­tal­lines appa­rais­sant dans la plu­part des cas à l’oc­ca­sion d’une trans­for­ma­tion péri­tec­tique, les voies les mieux adap­tées de fabri­ca­tion indus­trielle de qua­si-cris­taux sont les poudres obte­nues en tour d’a­to­mi­sa­tion où le refroi­dis­se­ment est suf­fi­sam­ment rapide pour évi­ter les tran­si­tions à forte ségré­ga­tion. Ces poudres peuvent ensuite être uti­li­sées à trois fins :

• revê­te­ment pour iso­la­tion thermique,
• ajout dis­per­soïde à effet dur­cis­sant dans des métaux à basse tem­pé­ra­ture de fusion,
• frit­tage et mou­lage haute tem­pé­ra­ture pour l’ob­ten­tion de pièces mas­sives qua­si cris­tal­lines aus­si bien en tant que maté­riaux de struc­ture (socles d’axes de petits rotors rapides) que de maté­riaux de fonc­tion pour leurs pro­prié­tés élec­tro­niques (ther­mo­ré­sis­tances basse température).

Ain­si, du point de vue des appli­ca­tions, les qua­si-cris­taux devraient trou­ver une niche tech­no­lo­gique dans le cadre des maté­riaux de struc­ture et de fonc­tion pour­vu que ces obs­tacles de fabri­ca­tion et de maî­trise métal­lur­giques soient défi­ni­ti­ve­ment fran­chis. Mais, au-delà des maté­riaux eux-mêmes, la décou­verte de Dany Shecht­man a per­mis de démar­rer de nom­breuses études mathé­ma­tiques et phy­siques d’ob­jets qua­si pério­diques abs­traits dont cer­taines sont sus­cep­tibles de retom­bées en aval.

Par exemple, comme il est main­te­nant facile de construire dans le plan des ensembles de points de symé­trie de rota­tion d’ordre fini quel­conque par­fai­te­ment ordon­nés, on peut en simu­ler numé­ri­que­ment les pro­prié­tés vibra­tion­nelles ou pro­pa­ga­tives, par exemple, celles des ondes élec­tro­ma­gné­tiques. Dans l’hy­po­thèse de pro­prié­tés inté­res­santes (ouver­ture d’un gap pho­to­nique par exemple), il est pos­sible d’en faire des réa­li­sa­tions concrètes par les pro­cé­dés de pho­to­gra­vure à des échelles micro­niques, voire nano­mé­triques, pour enri­chir la pano­plie d’ob­jets arti­fi­ciels uti­li­sables dans la microélectronique.

Comme l’on voit, la décou­verte des qua­si-cris­taux a engen­dré une mul­ti­tude de ques­tions fon­da­men­tales depuis celle d’une redé­fi­ni­tion de la notion d’ordre dans les solides, du trai­te­ment des spectres de struc­tures élec­tro­niques des milieux qua­si pério­diques jus­qu’aux pro­blèmes métal­lur­giques de la maî­trise de ces com­po­sés. Les solu­tions actuelles montrent de sub­stan­tiels pro­grès mais se heurtent encore à des dif­fi­cul­tés tant concep­tuelles qu’expérimentales.

Le temps du » easy work » est dépas­sé depuis plu­sieurs années et la recherche fon­da­men­tale se consacre main­te­nant à la mise au point de tech­niques spé­ci­fiques de spé­cia­listes. On constate qu’a­près une longue et fruc­tueuse période de recherches inten­sives aux USA et en France, les efforts se sont inten­si­fiés aujourd’­hui prin­ci­pa­le­ment au Japon et en Alle­magne où sont enga­gés de vastes pro­grammes de recherche sur le sujet : les qua­si-cris­taux pro­cèdent d’une démarche à long terme à laquelle la France par­ti­cipe très activement.

_____________________________________________
1. D. Shecht­man, I Blech, D. Gra­tias & J. W. Cahn, Phys. Rev. Lett. 53, 1951–1953 (1984).
2. D. Levine & P. J. Stein­hardt, Phys. Rev. Lett. 53, 2477–2480 (1984).
3. M. Duneau & A. Katz, Phys. Rev. Lett. 54, 2688–2691 (1985) – A. Katz & M. Duneau, J. Phys. France 47, 181–196 (1986).
4. H. Bohr, Acta Math. 45, 29 (1924) ; ibid. Acta Math. 46, 101 (1925) ; ibid. Acta Math. 47, 237 (1926).
5. A. S. Besi­co­vitch, Almost per­io­dic func­tions, Cam­bridge Uni­ver­si­ty Press UK (1932).
6. P. A. Kalu­gin, A. Y. Kitayev & L. S. Levi­tov, JETP Lett. 41, 145 (1985).
7. V. Elser, Acta Cryst. A 42, 36 (1986).
8. R. Pen­rose, Mathe­ma­ti­cal Intel­li­gen­cer 2, 32 (1979).
9. L. Ben­ders­ky, Phys. Rev. Lett. 55, 1461–1463 (1985).
10. A.-P. Tsai, A. Inoue & T. Masu­mo­to, Jpn J. Appl. Phys. 26, L1505-L1507 (1987) ; A.-P. Tsai, A. Inoue, Y. Yokoya­ma & T. Masu­mo­to, Mater. Trans., Jpn. Inst. Met. 31, 98 (1990).
11. S. Lyon­nard, G. Cod­dens, Y. Cal­vay­rac & D. Gra­tias, Phys. Rev. B 53, 3150–3160 (1996).

---

Articles similaires :

Avant pro­pos, par Roald HOFFMANN, prix Nobel de chi­mie 1981 Chro­no­lo­gie du demi-siècle écoulé La chi­mie quantique Où va l’industrie chimique 2011, année inter­na­tio­nale de la chimie