Covid-19 : interrogations sur le modèle épidémiologique,
Prise en compte de la vaccination et du « variant anglais »

Le modèle épi­dé­mio­lo­gique de base pro­po­sé en 1927 par Ker­mack et McKen­drick inclut une équa­tion inadap­tée aux phé­no­mènes dyna­miques qui est tou­jours ensei­gnée aux étu­diants du monde entier. Ne serait-ce pas une des rai­sons pour les­quelles, pen­dant l’été 2020, la plu­part des modé­li­sa­teurs avaient sous-esti­mé la vigueur de la « deuxième vague » d’octobre-novembre ?

Après cor­rec­tion de cette erreur presque cen­te­naire, quels ensei­gne­ments tirer pour 2021 d’une simu­la­tion très simple qui pren­drait en compte les évé­ne­ments nou­veaux que sont l’arrivée des vac­cins et celle du « variant anglais », cause poten­tielle d’une inquié­tante « nou­velle vague » ?

N.B. Les lec­teurs qui ne sont pas spé­cia­le­ment inté­res­sés par les tech­niques de modé­li­sa­tion peuvent aller direc­te­ment à la deuxième par­tie inti­tu­lée « Consé­quences de la vac­ci­na­tion et de l’arrivée du « variant anglais »

Les diri­geants du monde entier prennent leurs déci­sions de poli­tique sani­taire en tenant compte de résul­tats de simu­la­tions dont la plu­part, si on les exa­mine de près, sont encore basées, au moins par­tiel­le­ment, sur le sché­ma du modèle dit « com­par­ti­men­tal » ou « SIR » pro­po­sé à la Royal Socie­ty de Londres par Ker­mack et McKen­drick en 1927 ¹. Or la modé­li­sa­tion cor­res­pon­dante repose sou­vent sur une de ses équa­tions, inadap­tée à la simu­la­tion de phé­no­mènes évo­luant de façon dyna­mique. On peut sup­po­ser que ce choix a été dic­té par de pures rai­sons de com­mo­di­té de cal­cul à une époque où les ordi­na­teurs n’existaient pas.

De là a peut-être résul­té au cours de l’été 2020 pour la Covid-19 la pré­vi­sion erro­née d’une « deuxième vague » à crois­sance lente, de nom­breux experts conti­nuant à uti­li­ser dans leurs modèles cette équa­tion, encore ensei­gnée sans aucune mise en garde dans pra­ti­que­ment tous les cours d’épidémiologie. Les faits ont démen­ti cette pré­vi­sion et contraint de nom­breux gou­ver­ne­ments à décré­ter en catas­trophe ce qu’ils vou­laient évi­ter à tout prix, c’est-à-dire un deuxième confinement.

Dans une pre­mière par­tie, cette note montre qu’en fai­sant l’hypothèse que les carac­té­ris­tiques du virus ont peu varié jusqu’à la fin de 2020, le rem­pla­ce­ment de l’équation liti­gieuse par une autre, tout aus­si simple mais adap­tée à la simu­la­tion de sys­tèmes dyna­miques, per­met, en uti­li­sant un simple tableur infor­ma­tique, de com­prendre la sévé­ri­té de la reprise de l’épidémie en octobre-novembre.

Dans une deuxième par­tie, la même méthode décrit le chan­ge­ment radi­cal de pers­pec­tive induit en 2021 par l’arrivée de nou­veaux acteurs : des vac­cins effi­caces et des « variants » de forte contagiosité.

De façon géné­rale, il serait sou­hai­table qu’à l’avenir l’ensemble des épi­dé­mio­lo­gistes qui uti­lisent des modèles com­par­ti­men­taux ins­pi­rés par la com­mu­ni­ca­tion de 1927 de Ker­mack et McKen­drick cor­rigent l’équation inadap­tée aux régimes dyna­miques qui y figure.

PREMIERE PARTIE

I – Contexte 

Le célèbre modèle à trois « com­par­ti­ments » dit SIR (Sus­cep­tibles d’être infec­tés, Infec­tés , Réta­blis et décé­dés ), dont s’inspirent depuis 1927 la plu­part des épi­dé­mio­lo­gistes du monde entier, contient une équa­tion inadap­tée aux varia­tions rapides du nombre d’individus infec­tés. Vrai­sem­bla­ble­ment Ker­mack et McKen­drick n’ont pas choi­si la forme de cette équa­tion pour sa per­ti­nence, mais plu­tôt parce qu’à cette époque ils ne dis­po­saient pas de moyens de cal­cul infor­ma­tiques per­met­tant de trou­ver faci­le­ment de solu­tion à une autre équa­tion qui aurait mieux ren­du compte des phé­no­mènes bio­lo­giques réels. Conti­nuer à uti­li­ser l’équation de 1927 conduit à gra­ve­ment sous-esti­mer la dyna­mique d’une épi­dé­mie à des moments cru­ciaux tels que son déve­lop­pe­ment ini­tial, les effets d’un éven­tuel confi­ne­ment et la reprise des infec­tions qui peut suivre tout déconfinement.

Le main­tien de ce qu’on peut appe­ler « l’approximation de 1927 » au niveau mon­dial, que ce soit dans l’ensemble des cours d’épidémiologie ou dans de nom­breux modèles contem­po­rains, n’est guère com­pré­hen­sible à notre époque. Ce res­pect d’une for­mu­la­tion tra­di­tion­nelle de plus de quatre-vingt-dix ans, aujourd’hui dépas­sée, pour­rait expli­quer pour­quoi, dans de nom­breux pays, les modèles exis­tants avaient anti­ci­pé une vitesse de mon­tée de la « deuxième vague » de l’épidémie beau­coup plus faible que celle qui a été consta­tée à par­tir de septembre.

Par ailleurs, l’absence d’une prise en compte de la dyna­mique réelle d’une épi­dé­mie par les modèles uti­li­sant « l’approximation de 1927 » conduit à sous-esti­mer la rapi­di­té avec laquelle le nombre de per­sonnes infec­tées dimi­nue à la suite de mesures fai­sant bais­ser de façon dras­tique le coef­fi­cient de repro­duc­tion R₀.

Si l’approximation erro­née, base de l’équation de 1927, per­siste dans la plu­part des modèles, les pré­vi­sions d’évolution de l’épidémie actuelle dans dif­fé­rents scé­na­rios de confi­ne­ment et de décon­fi­ne­ment risquent être inexactes ; elles peuvent conduire les pou­voirs publics à prendre des déci­sions inadap­tées à la situa­tion réelle. Il est donc urgent de com­pa­rer les résul­tats don­nés par les modèles actuels, dont le détail du fonc­tion­ne­ment interne n’est géné­ra­le­ment pas dif­fu­sé, à ceux pro­ve­nant de modèles simples basés sur une ver­sion rec­ti­fiée de l’équation de 1927.

II – L’approximation de 1927 

Le modèle de Ker­mack et McKen­drick dit « SIR com­par­ti­men­tal » date de 1927. Depuis cette date il a ins­pi­ré les innom­brables modé­li­sa­teurs d’épidémies qui ont cher­ché à y ajou­ter de mul­tiples raf­fi­ne­ments, sans remettre en cause le modèle de base.

Qu’écrivent Kermack et McKendrick dans leur « Contribution à la théorie mathématique des épidémies » de 1927 ? 

Au début de cette « contri­bu­tion » ils expliquent qu’à un ins­tant don­né l’ensemble des indi­vi­dus malades com­prend plu­sieurs sous-ensembles, cha­cun d’entre eux incluant ceux ont été infec­tés pen­dant le même inter­valle de temps (et ont donc la même « ancien­ne­té » dans la maladie).

Figure alors le dia­gramme suivant :

qui laisse sup­po­ser que le moment où chaque malade a été infec­té sera pris en compte dans le modèle pour déter­mi­ner le moment où il sor­ti­ra de son état infec­tieux par gué­ri­son ou décès.

Mal­heu­reu­se­ment la dizaine de pages de cal­cul qui suivent, pra­ti­que­ment incom­pré­hen­sibles, ne per­met pas de voir s’ils sont arri­vés à une méthode de cal­cul (à l’époque sans l’aide d’ordinateurs !) per­met­tant de modé­li­ser une épi­dé­mie sui­vant ce principe.

Vrai­sem­bla­ble­ment dans la recherche du Graal qu’aurait été à cette époque la décou­verte d’une solu­tion expri­mable de façon ana­ly­tique, Ker­mack et McKen­drick pro­posent alors ce qu’ils appellent un « spe­cial case » :

Ces équa­tions sont à la base de la plu­part des mul­tiples sys­tèmes de simu­la­tion d’épidémies pro­po­sés depuis cette époque, avec des nota­tions qui sont habituellement :

dR / dt = – β S I

dI / dt = β S I – γ I

dR / dt = γ I ( voir plus bas la défi­ni­tion de ces lettres )

S + I + R = N

Elles tra­duisent les hypo­thèses suivantes :

1 – dans une popu­la­tion com­po­sée de N indi­vi­dus, dès que le nombre I de malades répu­tés infec­tieux le jour J est assez grand pour qu’on puisse appli­quer des méthodes sta­tis­tiques, le nombre de nou­veaux malades sup­plé­men­taires qui seront conta­mi­nés pen­dant ce jour J est pro­por­tion­nel à I et à S, ce qui s’exprime par l’équation :

Nombre quo­ti­dien de nou­veaux infec­tés = β x S x I (pro­duit des 3 nombres)

R₀ est le nombre de per­sonnes qu’infecte pen­dant toute la durée de sa conta­gio­si­té un malade plon­gé dans une popu­la­tion entiè­re­ment sus­cep­tible d’être infectée

β est pro­por­tion­nel à R₀ , très exac­te­ment : β = R₀ / (N x D).

N est la popu­la­tion totale et D le temps moyen pen­dant lequel une per­sonne malade est contagieuse

S est le nombre de per­sonnes pou­vant encore être conta­mi­nées (donc n’ayant été ni infec­tées, ni vac­ci­nées, et ne dis­po­sant pas d’une éven­tuelle immu­ni­té naturelle)

I est le nombre de per­sonnes infec­tieuses le jour J

Cette équation n’appelle pas de remarque particulière. 

2- pen­dant ce même jour J, le nombre de malades qui arrêtent, suite à leur gué­ri­son ou à leur décès, d’être sus­cep­tibles de conta­mi­ner des per­sonnes saines (et non immu­ni­sées par vac­ci­na­tion ou immu­ni­té natu­relle) est pro­por­tion­nel au nombre total de malades infectieux.

Nombre quo­ti­dien de per­sonnes infec­tées gué­ries (et immu­ni­sées) ou décé­dées = γ x I
(ne pou­vant donc plus conta­mi­ner d’autres personnes)

γ est l’inverse de D, temps moyen pendant
lequel une per­sonne malade est contagieuse

Cette approxi­ma­tion qui date de 1927, bien adap­tée à des phé­no­mènes sta­tiques ou qua­si-sta­tiques, ne rend pas compte cor­rec­te­ment de la dyna­mique réelle d’une épi­dé­mie, en par­ti­cu­lier dans les moments cru­ciaux que sont l’arrivée de la mala­die et le début ou la fin d’un confinement. 

En effet, pen­dant une période de crois­sance du nombre d’individus infec­tés, au jour J ceux-ci sont répar­tis en D sous-ensembles :

Le nombre d’infectés aug­mente de jour en jour. 

La taille de chaque case est pro­por­tion­nelle au nombre d’individus qu’elle contient. 

Dans la réa­li­té, les malades gué­rissent ou décèdent en moyenne D jours après avoir été infec­tés. Le jour J, dans une modé­li­sa­tion cor­recte, quittent donc le « com­par­ti­ment I des infec­tés » (par gué­ri­son ou décès) les malades, peu nom­breux (voir sché­ma) qui sont infec­tés depuis D jours.

L’ « approxi­ma­tion de 1927 » de Ker­mack et McKen­drick reprise dans tous les cours d’épidémiologie et la plu­part des modèles actuels fait sor­tir quo­ti­dien­ne­ment du « com­par­ti­ment I des infec­tés » la moyenne entre les D cases du dia­gramme ci-des­sus, c’est-à-dire un nombre très supé­rieur à la réa­li­té puisque les infec­tés récents sont arri­vés à un rythme quo­ti­dien de plus en plus élevé

Majo­rant le nombre de sor­ties du « com­par­ti­ment I » par rap­port au nombre réel, ce type de modèle dimi­nue arti­fi­ciel­le­ment la vitesse de crois­sance pré­vue pour une épi­dé­mie, par exemple à son début ou pen­dant une phase de déconfinement. 

Dans un modèle digne de ce nom, qui doit simu­ler une situa­tion en per­ma­nence évo­lu­tive, si D est la durée moyenne entre début d’infection et gué­ri­son ou décès, chaque jour le nombre de malades qui arrêtent d’être sus­cep­tibles de conta­mi­ner des per­sonnes saines est sen­si­ble­ment égal à celui des per­sonnes qui sont tom­bées malades D jours plus tôt (ce qui peut appa­raître comme une lapa­lis­sade, mais cer­tains paraissent l’ignorer … !).

Cette logique est très dif­fé­rente de celle adop­tée par Ker­mack et McKen­drick en 1927. Ce qu’on peut appe­ler « l’approximation de 1927 » abou­tit à ce qu’en phase de crois­sance le modèle SIR clas­sique comp­ta­bi­lise comme sor­tant de l’infection des indi­vi­dus qui sont tom­bés malades il y a net­te­ment moins de D jours, ce qui va conduire à la pré­vi­sion d’une crois­sance de l’épidémie très infé­rieure à la réa­li­té par sous-esti­ma­tion du nombre de per­sonnes res­tant infec­tieuses (c’est vrai­sem­bla­ble­ment ce qui est arri­vé en France à l’automne 2020, quand la « 2ème vague » Covid-19 a été beau­coup plus rapide et beau­coup plus forte que les pré­vi­sions de l’été, pen­dant lequel le très faible nombre de nou­veaux infec­tés quo­ti­diens avait même conduit cer­tains à annon­cer que l’épidémie était terminée).

Ce fait est connu de cer­tains modé­li­sa­teurs, mais ils ne semblent pas en avoir mesu­ré les consé­quences, qu’il est pos­sible d’évaluer par simu­la­tion de la même épi­dé­mie en uti­li­sant suc­ces­si­ve­ment un pro­gramme basé sur « l’approximation de 1927 » et un pro­gramme ayant rem­pla­cé l’équation cor­res­pon­dante (dR / dt = γ I) par une équa­tion adap­tée à la simu­la­tion de phé­no­mènes en régime for­te­ment dyna­mique (dR(t) / dt = – dS(t‑D) / dt). 

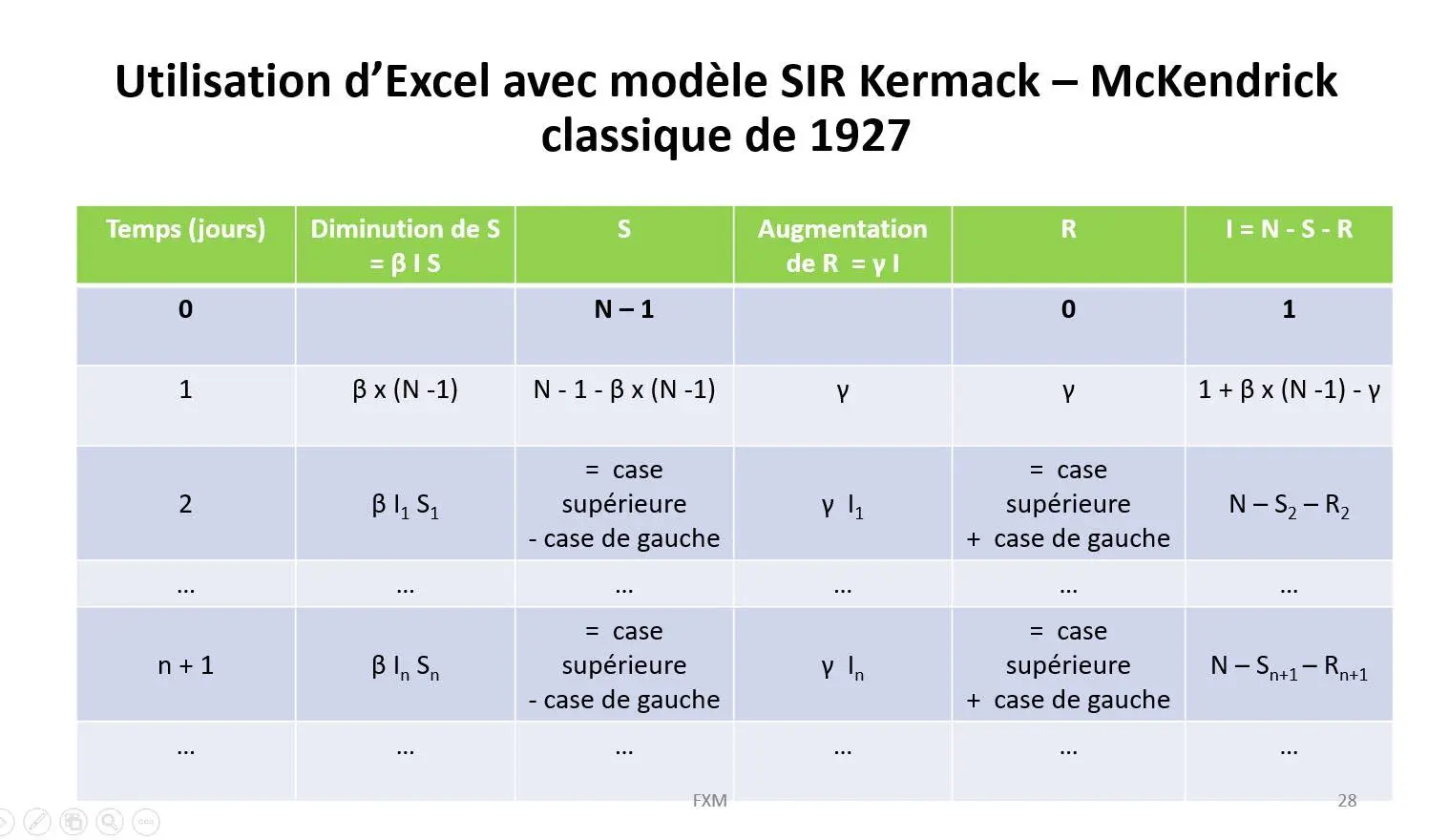
Pour ce faire, il est pos­sible d’utiliser un simple tableur qui per­met d’exprimer faci­le­ment le nombre de nou­veaux infec­tés, gué­ris et décé­dés en fonc­tion du nombre de de per­sonnes infec­tées, gué­ries et décé­dées pen­dant les jour­nées pré­cé­dentes et de l’évolution de cer­tains para­mètres (en par­ti­cu­lier R₀). L’exemple choi­si est un cas théo­rique sou­vent pré­sen­té dans les cours d’épidémiologie (R₀ = 3 et durées d’infection fixes pou­vant aller d’une à trois semaines ; voir en annexe les tableaux per­met­tant de simu­ler sim­ple­ment cette épi­dé­mie en uti­li­sant les 2 modèles). On l’applique à une popu­la­tion de 67 mil­lions d’habitants.

Uti­li­sons tout d’abord l’équation clas­sique de 1927 : dR / dt = γ I

A noter qu’il s’agit de simu­la­tions à R₀ constant uni­que­ment des­ti­nées à démon­trer la gra­vis­sime sous-esti­ma­tion du modèle de 1927 en phase de crois­sance d’une pan­dé­mie. Bien évi­dem­ment, si la mala­die est dan­ge­reuse, pou­voirs publics et popu­la­tion feront tout pour que R₀ dimi­nue avant que le nombre réel d’infectés atteigne le maxi­mum théo­rique de ces courbes. D’autre part, au cours d’une épi­dé­mie réelle, R₀ varie en per­ma­nence pour de mul­tiples rai­sons tenant tout à la fois au com­por­te­ment de la popu­la­tion et à des don­nées médi­cales (muta­tions éven­tuelles du virus, décou­verte de trai­te­ments chan­geant la durée de conta­gio­si­té des per­sonnes infec­tées). L’accent qua­si exclu­sif mis dans les cours d’épidémiologie sur des cas théo­riques d’épidémies à R₀ constant pou­vait se jus­ti­fier à l’époque où, faute d’ordinateurs, il était impor­tant d’essayer de trou­ver des résul­tats expri­mables sous forme de fonc­tions ana­ly­tiques. L’important de nos jours est d’utiliser des équa­tions repré­sen­tant le mieux pos­sible le phé­no­mène que l’on veut simu­ler : ensuite, de toute façon, le cal­cul (par ordi­na­teur) suivra ! 

A R₀ constant (égal à 3) le pic théo­rique (voir plus haut) du nombre d’infectés (21 mil­lions sur une popu­la­tion de 67 mil­lions) cor­res­pon­dant à l’atteinte de ce qu’on appelle « l’immunité col­lec­tive » dépend très peu de la durée d’infection moyenne. En revanche, le nombre quo­ti­dien maxi­mal théo­rique de nou­velles infec­tions est plus impor­tant (4 mil­lions / jour) dans le cas d’une durée d’infectiosité courte (7 jours) que dans le cas d’une infec­tio­si­té plus longue (1,5 mil­lion / jour pour D = 20 jours).

Uti­li­sons main­te­nant l’équation dR(t) / dt = – dS(t‑D) / dt , D durée de la période d’infection conta­gieuse étant égale à 1 / γ

Cer­taines conclu­sions sont les mêmes que celles résul­tant de l’utilisation de l’équation de 1927 : 

A R₀ constant (égal à 3) le pic théo­rique du nombre d’infectés (37 mil­lions sur une popu­la­tion de 67 mil­lions, cor­res­pon­dant à l’atteinte de l’immunité col­lec­tive) dépend très peu de la durée d’infection moyenne. En revanche, le nombre quo­ti­dien maxi­mal théo­rique de nou­velles infec­tions est plus impor­tant (6 mil­lions / jour) dans le cas d’une durée d’infectiosité courte (7 jours) que dans le cas d’une infec­tio­si­té plus longue (2 mil­lions / jour pour D = 20 jours).

On peut éga­le­ment remar­quer que c’est R₀ qui est déter­mi­nant pour le cal­cul du nombre maxi­mum d’infectés cor­res­pon­dant à l’atteinte de l’immunité col­lec­tive au-delà de laquelle l’épidémie com­mence à s’éteindre spon­ta­né­ment. A R₀ constant, une faible varia­tion de la durée moyenne d’infection D ne change pas de façon fon­da­men­tale l’évolution de l’épidémie (mais il faut bien sûr remar­quer que la valeur de D est déjà prise en compte dans l’égalité : R₀ = β D N = β N / γ )

Mais cer­taines dif­fé­rences sautent aux yeux : 

* le pic théo­rique du nombre d’infectés maxi­mal théo­rique don­née par l’équation rec­ti­fiée est beau­coup plus éle­vé que celui don­né par l’équation clas­sique de 1927 (37 mil­lions au lieu de 21 millions),

* l’équation rec­ti­fiée implique un décol­lage signi­fi­ca­tif de l’épidémie et une atteinte du nombre maxi­mal de per­sonnes conta­mi­nées net­te­ment plus rapides que l’équation de 1927

On peut mettre en évi­dence ces dif­fé­rences en por­tant sur le même dia­gramme les résul­tats obte­nus avec les 2 équa­tions dif­fé­rentes, par exemple pour R₀ = 3 et D = 10 jours :

Comme indi­qué plus haut, ces courbes ont un carac­tère théo­rique, car dans le cas d’une mala­die grave, R₀ va géné­ra­le­ment dimi­nuer rapi­de­ment sous l’influence de chan­ge­ments de com­por­te­ment de la popu­la­tion spon­ta­nés (réduc­tion des contacts avec les malades par peur de la conta­gion) ou impo­sés par les pou­voirs publics (confi­ne­ments, couvre feux, fer­me­ture de maga­sins et de salles de spectacles …).

Mais ce qui n’est pas seule­ment théo­rique est le fait que l’utilisation de l’équation de 1927, qui traite les gué­ri­sons et les décès comme s’il s’agissait d’un phé­no­mène phy­sique tel que la radio­ac­ti­vi­té, divise pra­ti­que­ment par deux les varia­tions (à la hausse comme à la baisse) des nombres d’infections cal­cu­lées par l’équation rec­ti­fiée qui, elle, tient compte de la réa­li­té bio­lo­gique d’une période d’infection variant rela­ti­ve­ment peu par rap­port à une valeur moyenne.

Sensibilité à R₀

Il est inté­res­sant de faire la même com­pa­rai­son entre les résul­tats obte­nus avec d’autres valeurs de R₀, telles que 1,5 qui est une valeur cou­ram­ment obte­nue pour l’épidémie Covid-19 sans confi­ne­ment, mais avec des mesures de dis­tan­cia­tion physique.

On retrouve les mêmes conclu­sions que pour R₀ = 3, avec des valeurs abso­lues plus petites.

Conclu­sions

L’équation de 1927, adap­tée aux seules situa­tions sta­tiques ou qua­si-sta­tiques, génère une solu­tion erronée : 

- les deux pics (nou­veaux infec­tés quo­ti­diens et total des per­sonnes infec­tées au jour J) sont égaux à un peu plus de la moi­tié de ceux don­nés par l’équation qui rend compte cor­rec­te­ment du phé­no­mène dyna­mique. De plus, ces pics sur­viennent avec retard. 

- en phase ascen­dante de l’épidémie, le taux de crois­sance du nombre d’infectés cal­cu­lé avec l’équation de 1927 est net­te­ment plus faible que celui décou­lant de l’équation « dynamique » 

Depuis l’arrivée de l’informatique, la contrainte résul­tant du choix sys­té­ma­tique d’équations condui­sant aux cal­culs les plus simples pos­sibles n’existe plus. La bonne méthode dans un tel cas est de conce­voir des équa­tions les plus proches pos­sibles des phé­no­mènes que l’on sou­haite simu­ler, et d’utiliser un sol­veur pour en trou­ver les solu­tions. Au pas­sage, ceci per­met de simu­ler faci­le­ment des épi­dé­mies où R₀ varie, ce qui est le cas dans toutes les épi­dé­mies réelles tout à la fois à la suite :

- d’évolutions spon­ta­nées (par peur) ou contraintes (confi­ne­ment) du com­por­te­ment de la population,

- ou d’éventuelles modi­fi­ca­tions de don­nées bio­lo­giques (muta­tions impor­tantes du virus, décou­verte de trai­te­ments plus efficaces).

Conclu­sion (qui n’est que la for­ma­li­sa­tion d’une lapalissade !) :

III – Simulation de l’épidémie Covid-19 avec un modèle SIR où l’équation dR/dt = γ I est remplacée par une équation adaptée aux phénomènes dynamiques : dR(t) / dt = – dS(t‑1/γ) / dt 

Compte tenu des nom­breux chiffres acces­sibles sur divers sites Inter­net, il est pos­sible d’introduire dans un tel modèle des para­mètres R₀ et D per­met­tant d’obtenir une bonne cohé­rence avec l’évolution obser­vée de l’épidémie.

D = 10 jours (soit γ = 0,1)

N = 67 000 000 S : nombre d’individus sus­cep­tibles d’être contaminés

R₀ évo­luant entre 0,7 et 3

R_effec­tif = R₀ x S / N

β = R₀ / (N x D)

1. jusqu’au 16 mars : R₀ = 3
2. baisse de 3 à 0,7 en 10 jours (début du 1er confi­ne­ment)
3. R₀ = 0,7 jusqu’au 10 mai (1er confi­ne­ment)
4. hausse linéaire de 0,7 à 1,5 en 133 jours (1er décon­fi­ne­ment)
5. R₀ = 1,5 du 23 sep­tembre au 22 octobre (fin du 1er décon­fi­ne­ment)
6. baisse de 1,5 à 0,95 en 10 jours (début du couvre-feu sui­vi du 2ème confi­ne­ment)
7. R₀ = 0,95 jusqu’au 14 décembre (2ème confi­ne­ment)
8. à par­tir du ¹⁵⁄₁₂ hausse linéaire sui­vant la même pente qu’en 4 (2ème décon­fi­ne­ment)

Com­pa­rai­son entre les pré­vi­sions de « 2ème vague » en uti­li­sant les deux types d’équations

On se place au 1er août avec les effec­tifs don­nés par le modèle uti­li­sant l’équation rec­ti­fiée pour :

- les infectés

- les per­sonnes sus­cep­tibles d’être infec­tées (en excluant donc les per­sonnes immu­ni­sées suite à leur gué­ri­son ain­si que les per­sonnes décédées).

Puis on demande aux tableurs uti­li­sant les deux types d’équations de don­ner l’évolution des infec­tions jusqu’à la fin de juin 2021.

On constate immé­dia­te­ment que le modèle uti­li­sant l’équation « dyna­mique » pré­voit à par­tir de sep­tembre une mon­tée beau­coup plus rapide du nombre de nou­veaux infec­tés quo­ti­diens que le modèle uti­li­sant l’équation de 1927, avec un pic théo­rique, en l’absence de nou­veau confi­ne­ment, de plus de 600 000 infec­tions quo­ti­diennes atteint dès décembre 2020. Le modèle fon­dé sur « l’approximation de 1927 » pré­voit une mon­tée net­te­ment plus lente avec un pic théo­rique de plus de 300 000 infec­tions quo­ti­diennes atteint en février 2021.

Là encore, l’équation « dyna­mique » est net­te­ment plus conforme à la réa­li­té obser­vée à l’automne 2020 que ce que pré­voyaient les modèles basés sur l’équation tra­di­tion­nelle de 1927.

Cas d’une décroissance du nombre d’infectés

Il convient de remar­quer que le carac­tère « dyna­mique » de l’équation pro­po­sée fonc­tionne dans les deux sens : il rend compte, en cas de confi­ne­ment ame­nant R en des­sous de 1, d’une dimi­nu­tion réelle du nombre d’infections net­te­ment plus forte que ce que laissent pré­voir les modèles basés sur l’équation de 1927.

En effet, en cas de décrois­sance du nombre d’infections, si on consi­dère l’ensemble des per­sonnes infec­tées au jour J, elles sont divi­sées en D sous-ensembles :

Le nombre d’infectés dimi­nue de jour en jour. 

La taille de chaque case est pro­por­tion­nelle au nombre d’individus qu’elle contient. 

L’ « approxi­ma­tion de 1927 » de Ker­mack et McKen­drick fait sor­tir quo­ti­dien­ne­ment du « com­par­ti­ment I des infec­tés » la moyenne entre les D cases du dia­gramme ci-des­sus, c’est-à-dire un nombre très infé­rieur à la réa­li­té puisque les infec­tés qui sortent réel­le­ment du com­par­ti­ment I sont ceux, nom­breux, qui sont arri­vés D jours auparavant.

Mino­rant le nombre de sor­ties du « com­par­ti­ment I », ce type de modèle dimi­nue arti­fi­ciel­le­ment la pré­vi­sion de la vitesse à laquelle une épi­dé­mie décroît, par exemple lorsqu’un confi­ne­ment fait pas­ser R_effec­tif en-des­sous de 1. 

Ceci donne une pos­sible expli­ca­tion, au moins par­tielle, de la dif­fé­rence entre la décla­ra­tion du Pré­sident Macron indi­quant le 28 octobre 2020 que, « quoi qu’on fasse », il allait y avoir 9 000 patients Covid-19 en réani­ma­tion le 15 novembre et le chiffre réel obser­vé à cette date, net­te­ment plus faible. Il se peut que l’ef­fet du couvre-feu (23 octobre) puis de 2^ème confi­ne­ment (29 octobre) ait été plus rapide que ce que pré­voyaient des modèles basés, au moins par­tiel­le­ment, sur l’équation de 1927.

IV – Conclusion 

L’équation pro­po­sée par Ker­mack et McKen­drick en 1927 pour le cal­cul du nombre de malades sor­tant d’infection par gué­ri­son ou décès n’est valable que si leur nombre est stable, ce qui dans la réa­li­té d’une épi­dé­mie n’est jamais le cas. Si on rem­place l’équation de 1927 par une autre tenant compte du carac­tère dyna­mique du flux de malades on constate que ceci induit une forte modi­fi­ca­tion des pré­vi­sions du modèle : par exemple à R₀ constant, l’équation de 1927 donne une pointe du nombre maxi­mum d’infectés deux fois plus faible que l’équation « dyna­mique » par laquelle elle devrait être rem­pla­cée pour être conforme à la réa­li­té, ain­si qu’un taux de crois­sance du nombre de per­sonnes infec­tées très inférieur.

Glo­ba­le­ment, l’équation de 1927 conduit à mini­mi­ser les futures varia­tions réelles du nombre d’infections. Elle est dan­ge­reuse pen­dant les phases où l’épidémie se déve­loppe, car elle peut conduire à sous-esti­mer les besoins futurs en équi­pe­ment et en per­son­nel médi­cal. Mais inver­se­ment cette carac­té­ris­tique joue dans l’autre sens pen­dant les phases de décé­lé­ra­tion, car fina­le­ment les actions des pou­voirs publics des­ti­nées à réduire le nombre de malades seront plus effi­caces, dès que R_effec­tif passe en-des­sous de 1, que ce qu’indique un modèle uti­li­sant l’équation de 1927. 

DEUXIEME PARTIE

Simu­la­tion des effets de la vac­ci­na­tion et de l’introduction du « variant anglais » pen­dant toute l’année 2021 

I – Simulation sans « variant anglais » 

Sans vaccination

Début 2021, le coef­fi­cient R_effec­tif est d’environ 1,2.

La part de la popu­la­tion sus­cep­tible d’être conta­mi­née (S/N ) don­née pour cette époque par le modèle uti­li­sé (SIR à durée d’infection constante) est 0,86.

R₀ = 1,2 / 0,86 = 1,4

Exa­mi­nons tout d’abord la situa­tion théo­rique où, sans modi­fi­ca­tion de R₀, il n’y aurait ni confi­ne­ment, ni vac­ci­na­tion. Il y aurait alors une « troi­sième vague » d’amplitude supé­rieure à celle des deux pré­cé­dentes (toutes deux ayant été inter­rom­pues par les deux pre­miers confi­ne­ments). L’amplitude de cette vague dépas­se­rait en mars-avril les capa­ci­tés d’accueil du sys­tème hos­pi­ta­lier. De toute évi­dence, les pou­voirs publics seraient ame­nés à mettre en place un troi­sième confinement.

Mais un fait nou­veau est sur­ve­nu début 2021 : la popu­la­tion a com­men­cé à être vaccinée.

Vaccination

La vac­ci­na­tion com­mence en jan­vier 2021. Devant les nom­breuses incer­ti­tudes sur le rythme de la vac­ci­na­tion, le délai d’apparition de l’immunité des vac­ci­nés, le décompte dif­fé­rent entre indi­vi­dus vac­ci­nés et nombre de doses, nous adop­tons dans un pre­mier temps une hypo­thèse simple : à par­tir du 20 jan­vier 100 000 per­sonnes par jour sont immu­ni­sées et quittent le « com­par­ti­ment » S sans pas­ser par « I ».

Le pre­mier sché­ma de la page sui­vante est un rap­pel du scé­na­rio sans vac­ci­na­tion où R₀ reste à son niveau de début de 2021 (1,4), ce qui cor­res­pond à R_effec­tif pas­sant pro­gres­si­ve­ment de 1,2 à 0,81.

Le deuxième sché­ma cor­res­pond à l’introduction d’une vac­ci­na­tion (100 000 immunisés/jour à par­tir du 20 jan­vier) qui fait bais­ser de façon signi­fi­ca­tive le nombre d’infectés en mars-avril. On se trouve alors dans une situa­tion où un confi­ne­ment moins strict (par exemple couvre-feu ren­for­cé, res­tric­tions de cer­tains dépla­ce­ments …) pour­rait être suffisant.

II – Simulation avec « variant anglais » 

Inté­grons dans les dia­grammes qui suivent l’arrivée d’un variant « anglais » (1,5 fois plus conta­gieux que le virus de type « 2020 »). Les der­niers chiffres connus à ce jour (27÷1÷2021) indiquent qu’au 8 jan­vier 2,5% des per­sonnes conta­mi­nées l’auraient été par un virus de type « anglais. D’après notre modèle, ceci cor­res­pond à un « patient zéro » arri­vant en France fin sep­tembre 2020 (ou plu­sieurs arri­vant à des dates postérieures).

Dans une telle situa­tion s’engage une com­pé­ti­tion entre « virus 2020 » et « variant anglais » pour conta­mi­ner les indi­vi­dus du com­par­ti­ment des « Sus­cep­tibles ». Grâce à sa conta­gio­si­té supé­rieure, le variant anglais prend le des­sus, fai­sant dis­pa­raître en quelques mois le virus 2020.

D’après notre modèle, la pro­por­tion d’infections « anglaises » par­mi l’ensemble des infec­tions Covid serait la suivante :

• 8 jan­vier : 2,5 %
• fin jan­vier : 14 %
• fin février : 60 %
• fin mars : 94 %

En l’absence de vac­ci­na­tion et d’une modi­fi­ca­tion de com­por­te­ment de la population

(R₀ res­tant égal à 1,4 pour le virus « 2020 », et par voie de consé­quence 2,1 pour le virus « anglais ») on se trou­ve­rait alors face à une catas­trophe sani­taire majeure.

La vac­ci­na­tion à 100 000 immu­ni­sés par jour per­met de réduire de façon signi­fi­ca­tive le nombre d’infectés, mais pas de façon suf­fi­sante en l’absence de mesures fai­sant simul­ta­né­ment bais­ser radi­ca­le­ment R0 « 2020 » jusqu’aux envi­rons de 1, les R_effec­tif pas­sant alors en-des­sous de 1.

Conclusion

Les simu­la­tions qui pré­cèdent, basées sur des hypo­thèses pré­li­mi­naires concer­nant le rythme des vac­ci­na­tions, leur effi­ca­ci­té, la conta­gio­si­té du « variant anglais », le com­por­te­ment de la popu­la­tion, qu’il soit spon­ta­né (peur de l’infection) ou contraint (sui­vi des consignes gou­ver­ne­men­tales) ne peuvent avoir valeur de pré­vi­sions tant que ces para­mètres ne sont pas connus avec plus de précisions.

En revanche, ces simu­la­tions per­mettent de bien com­prendre cer­tains méca­nismes de l’épidémie ain­si que les effets pré­vi­sibles de dif­fé­rentes déci­sions de poli­tique sani­taire. Elles montrent la sou­plesse du modèle simple uti­li­sé, qui peut être adap­té très rapi­de­ment à de nou­velles don­nées (nombre et carac­té­ris­tiques des variants, rythme et effi­ca­ci­té des vac­ci­na­tions, varia­tions com­por­te­men­tales de la population …).

ANNEXE

1. Ker­mack, W. O., McKen­drick, A. & Wal­ker, G. T. A contri­bu­tion to the mathe­ma­ti­cal theo­ry of epi­de­mics. Proc. R. Soc. A 115, 700–721. https://doi.org/10.1098/rspa.1927.0118 (1927).

---

Articles similaires :

« Deuxième vague » Covid-19 : pers­pec­tives 2020–2021 Covid-19 en 2021
Quelles mesures pri­vi­lé­gier pour évi­ter d’être sub­mer­gés en mars avril par l’arrivée d’une 3^e vague due au variant « anglais » ? La modé­li­sa­tion des épi­dé­mies à l’épreuve de la Covid-19 Covid-19 : pers­pec­tives d’infection par le variant Omicron Modèles mathé­ma­tiques d’épidémies les plus éla­bo­rés : pour­quoi leurs pré­vi­sions ini­tiales sont-elles sou­vent exces­si­ve­ment pessimistes ?